A soma do dobro de um número somado com 3 é maior que a diferença entre seu quádruplo menos 1. Este número pode ser:
- 1
- 2
- 3
- 4
Passo 1
Vamos lááá!! Primeiro passo pra resolver esse problema é entender o que o enunciado quer dizer e escrever isso no “matematiquês”, beleza?!

O enunciado diz pra gente: “A soma do dobro de um número somado com 3 é maior que a diferença entre seu quádruplo menos 1.”. Vamos chamar esse número desconhecido de ! Assim,
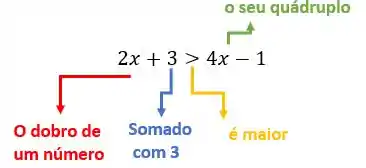
Ouuuu seja, a nossa inequação é
Show de bola?!
Passo 2
Agora isolar o para encontrar o seu valor! Primeira passaremos o para o lado esquerdo da desigualdade
Da mesma forma, passaremos o para o lado direito da desigualdade
Agora dividiremos ambos os lados por . Lembrando que quando dividimos por um número negativo precisamos inverter o sinal da inequação!!!
Portanto, analisando as alternativas, o único valor que é menor que é o 1. Nossa resposta então é a letra (a)