Encontre o conjunto solução para a inequação abaixo:
Passo 1
Fizemos uma parecida na teoria, lembra?
Vamos primeriamente tentar encontrar as raízes da equação. Simbora?
Opaaa! O é negativo, isso significa que não temos raízes reais.
E AGORA? QUEM PODERÁ NOS DEFENDER?

Passo 2
Olhando para o valor do a, vemos que ele é maior do que zero. Isso significa que a nossa função sempre será positiva. O esboço do nosso gráfico vai ficar assim, ó:
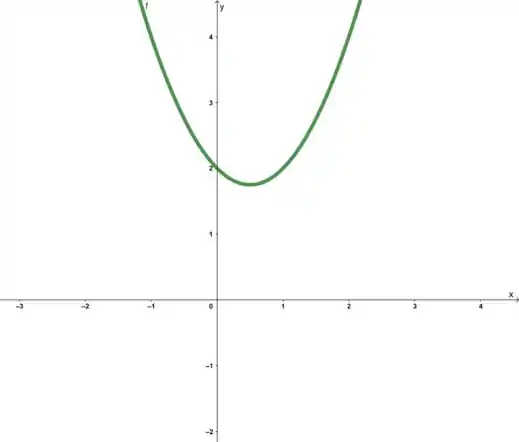
Como no enunciado queríamos os valores de x que tornam essa equação negativa, a resposta será: NENHUM rs
Ou seja, o conjunto solução será:
Obs: Ø Conjunto vazio