- Resolva a desigualdade
Encontre o conjunto solução e o ilustre sobre a reta real.
Passo 1
Olá, pessoal! Tudo bom? Aqui temos uma inequação para analisar e repara que ela está em módulo. Ou seja, essa desigualdade é equivalente a
Repara também que o denominiados dele tem um , ou seja, o domínio dela não será todos os reais, pois o denominador não pode ser zero, logo . Então vamos ter duas condições possíveis para ele
Agora vamos analisar cada caso!
Passo 2
Quando , temos:
Logo,
Analisando as desigualdades separadamente:
Para o outro lado,
Como . As regiões que serão satisfeitas são:
Ou seja, a desigualdade é valida para
Passo 3
Quando , temos:
Logo,
Analisando as desigualdades separadamente:
Para o outro lado,
Ou seja, a desigualdade é valida para
Passo 4
Unindo os resultados obtidos, temos que o conjunto solução é .
Na notação de intervalo: .
E a figura fica assim,
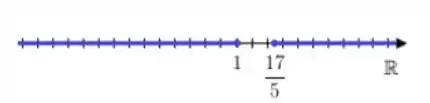
Resposta