Resolva em as inequações abaixo:
c)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu a inequação de segundo grau e pediu pra gente encontrar os valores de para os quais elas estão definidas no conjunto dos números reais (em ).
Então, o que nós vamos fazer é encontrar as raízes de cada equação, pra a partir daí montar o gráfico e verificar os intervalos onde a função é negativa ou positiva. Em seguida, nós vamos montar um quadro e fazer o estudo de sinal de cada produto e ver quais os intervalos que satisfazem a inequação.
Vamos lá!
Passo 2
No item c),
Vamos separar cada equação e encontrar suas raízes e seus gráficos. Começando com:
Usando Bhaskara, obtemos:
Esboçando o gráfico:
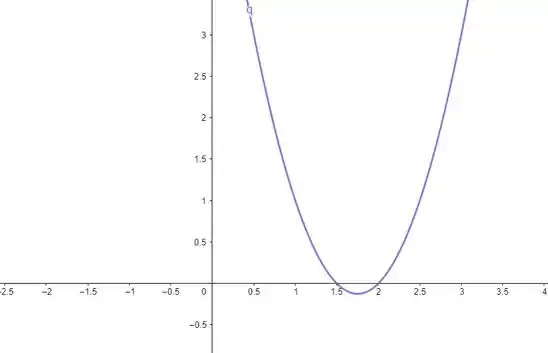
Repara que a nossa função só é negativa quando ela corta o eixo de até . Então, temos o intervalo:
Percebeu que agora a gente utilizou os colchetes? É porque a nossa inequação nos diz que o produto das funções é menor ou igual a zero. Se ele pode ser zero, nós incluímos as raízes da função (onde ela zera) e temos um intervalo fechado.
Passo 3
Agora vamos analisar a equação:
Encontrando suas raízes:
Esboçando o gráfico:
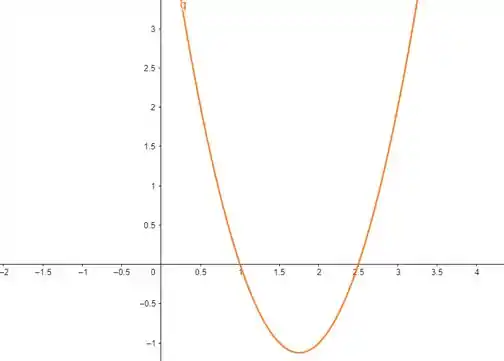
O gráfico é bem parecido com a equação anterior. Repara que ele é negativo apenas de até . Então, nosso intervalo é:
Por fim, temos a reta:
Isolando pra descobrir onde ela corta o eixo, temos:
E seu esboço fica assim:
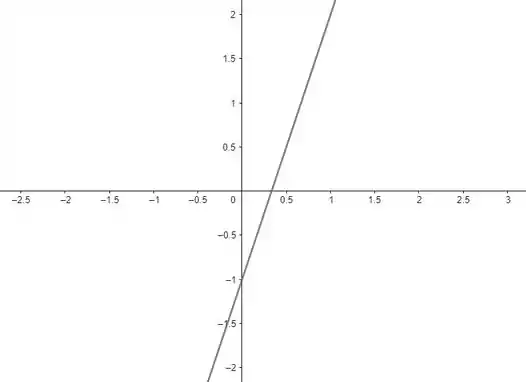
A reta é negativa até e depois passa a ser positiva. Então, o intervalo onde ela é negativa é:
Beleza, agora vamos fazer o estudo de sinais dessas três equações:
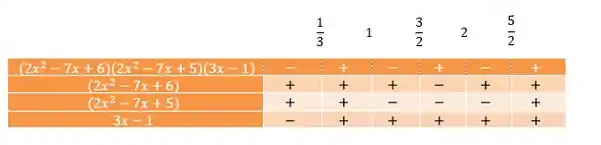
Como queremos:
Vamos selecionar os intervalos onde o sinal é negativo (olhando pra primeira linha da tabela). Assim, o nosso conjunto solução é:
Prontinho, galera! Até a próxima! 😉