Resolva as inequações dos exercícios 1 a 12.
5.
Passo 1
Oi, galerinha! Tudo bom? Nessa questão, vamos resolver essa inequação. E repara que ela é um produto de polinômions do primeiro grau.
Então, galerinha, quando tivermos essa situação, o que faremos é seguir os passos bem parecidos com o de uma equação, mas ao invés de uma igualdade, vamos ter um sinal de maior ou menor na nossa inequação, para cada termo. E depois faremos o estudo do sinal.
Bora lá!
Passo 2
O problema nos forneceu a seguinte inequação,
Começando pelo termo
Para
Por fim, temos
Agora vamos montar uma tabelinha e fazer o estudo do sinal.
Passo 3
Então, pessoal, o que vamos fazer aqui é anisar os intervalos onde o termo é positivo e negativo.
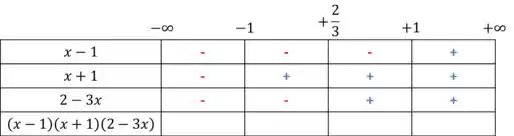
Agora, vamos fazer a multiplicação dos sinais em cada coluna, e saber o sinal é menor ou maior que zero.
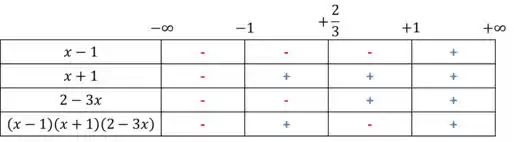
Ou seja, ela será menor que nos intervalos e .
A solução será, portanto: