Resolva em as inequações abaixo:
k)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu algumas inequações (que são equações que não possuem igualdade, lembra?) e pediu pra gente resolver dentro do conjunto dos números reais, ou seja, em . Tá, mas como a gente resolve isso?
Resolve-las significa encontrar os valores de que satisfazem essa condição de desigualdade. No nosso caso, a condição no item k) é:
Quando nós temos um quociente e uma desigualdade, nós precisamos avaliar os sinais tanto do numerador, quanto do denominador, que satisfaçam aquela condição.
Nós temos uma relação maior ou igual a que zero. Dessa forma, nós vamos escrever todo mundo no mesmo denominador e avaliar cada caso para encontrar os valores de que satisfaçam a condição de desigualdade.
Vamos lá!
Passo 2
Vamos começar colocando todo mundo do lado direito no mesmo denominador, tirando o m.m.c.:
Agora vamos subtrair dos dois lados:
Tirando o m.m.c. de novo, temos:
Podemos simplificar dividindo os dois lados por :
Passo 3
Beleza, agora temos a condição desse quociente ser maior ou igual a zero. Isso vai acontecer quando numerador e denominador tiverem sinais iguais, certo? Lembrando que o denominador nunca pode ser zero.
Logo, temos no primeiro caso:
Vamos encontrar onde essas funções cortam o eixo fazendo:
Encontramos:
Vamos dá uma olhadinha no gráfico: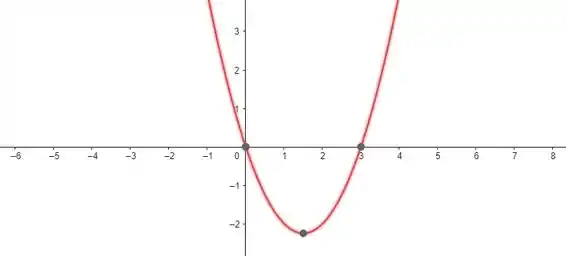
Repara que essa função é positiva de e em . Ou seja:
Passo 4
No caso de , podemos separar as três retas pra ver onde elas são positivas:
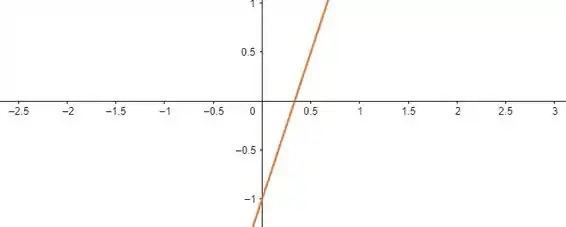
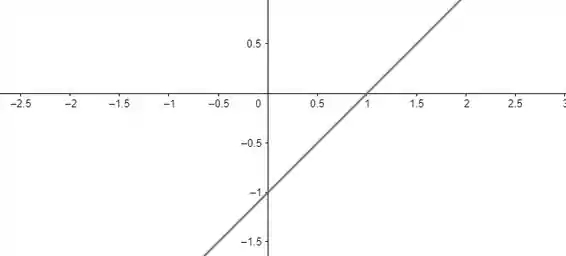
E por fim,
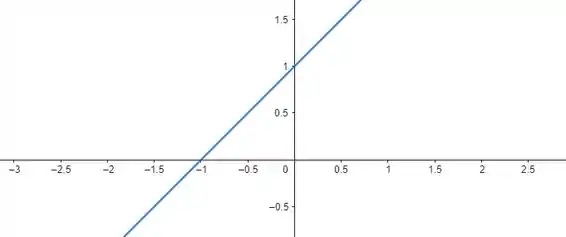
Repare que as três são positivas depois que atravessam o eixo , beleza? Também poderíamos satisfazer a inequação, fazendo:
As raízes e os gráficos não mudam, o que muda é que agora a gente consideraria os intervalos onde essas funções são negativas. Vamos juntar tudo numa tabelinha pra fica melhor.
Passo 5
Fazendo estudo de sinal de cada função, temos:
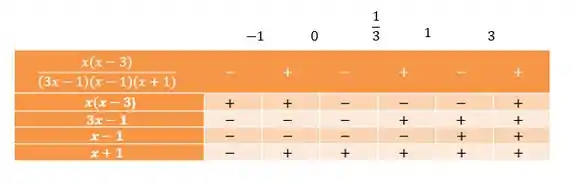
Como queremos que a nossa equação seja maior ou igual a zero:
Vamos selecionar os intervalos em que é positivo (ou nulo) olhando para a primeira linha da tabela. E temos nosso conjunto solução:
Prontinho, galera! Até a próxima! 😉