UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 9, Questão 3
Resolva em as inequações simultâneas abaixo:
a)
b)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu algumas inequações simultâneas e pediu pra gente encontrar os valores de para os quais ela está definida no conjunto dos números reais (em ).
Então, o que nós vamos fazer é resolve-las por partes. Primeiro vamos pegar um lado da desigualdade, depois o outro. Assim, vamos avaliar o sinal e encontrar um conjunto solução em cada caso. A interseção desses dois conjuntos será nossa solução geral.
Vamos lá!
Passo 2
No item a), temos a inequação:
Vamos pegar primeiro a desigualdade do lado esquerdo:
Subtraindo dos dois lados, temos:
Isolando , nós conseguimos encontrar as raízes da equação:
Esboçando o gráfico, temos:
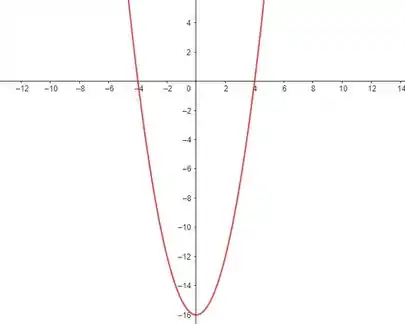
Repare que ela começa positiva e, somente depois que passa por , ela se torna negativa. Nós estamos interessados em onde a função é positiva, já que essa é a condição da inequação que encontramos.
Assim, temos o intervalo:
Passo 3
Olhando agora pro lado direito da inequação , temos:
Encontrando as raízes dessa equação:
O gráfico dessa equação fica assim:
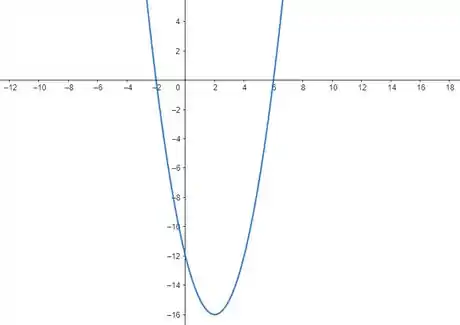
Repare que ela negativa somente no intervalo , que é fechado porque nossa desigualdade também incluir o valor da função em zero. Assim, temos:
A interseção dos dois conjuntos (que são os elementos que pertencem simultaneamente aos dois) forma nossa solução geral. Ou seja,
Agora vamos pra o próximo item.
Passo 4
No item b), temos a desigualdade simultânea:
Olhando só pro lado esquerdo, temos:
Podemos multiplicar os dois lados por invertendo o sinal da desigualdade:
Agora vamos avaliar sua equação:
Que nos fornece as raízes:
Plotando esse gráfico, temos:
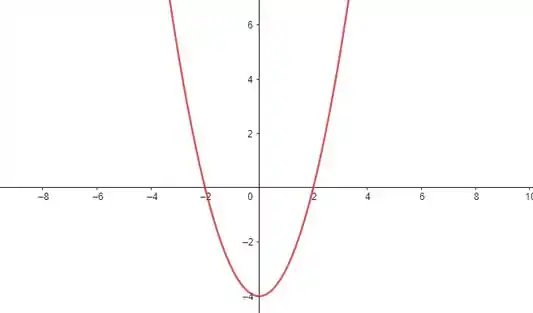
Repare que essa função vai ser menor ou igual a zero no intervalo:
Agora vamos olhar o outro lado da inequação:
Arrumando fica:
Vamos calcular as raízes dessa equação e esboçar seu gráfico também. Temos:
Esboçando o gráfico:
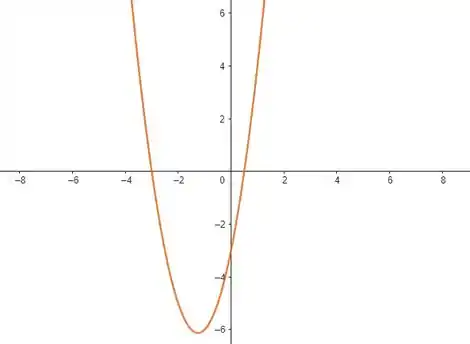
Vamos olhar agora pra onde a função é negativa, quando ela tá abaixo do eixo . Nesse caso, temos o intervalo:
A interseção de e vai nos dá nosso conjunto solução. A gente sempre tem que se perguntar onde estão os elementos que estão em e ao mesmo tempo? Nesse caso, será:
Prontinho, galera! Até a próxima! 😉
Resposta
a)
b)