UFES, 2018.1, Lista 3, Q05c
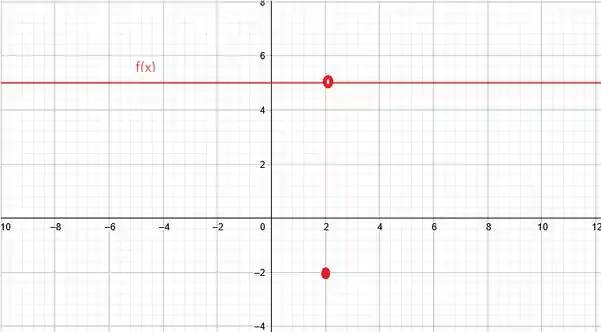
5c) Sabe-se que e é definida em Todas as afirmativas abaixo são falsas. Tente desenhar um contraexemplo para cada uma delas.
é positivo
Passo 1
Fala pessoal, vamos continuar a solução dessa questão!!
A ideia aqui é bem parecida com o item b). Primeiramente, essa afirmação é falsa porque como podemos criar funções descontínuas em , o valor de nessa descontinuidade pode ser literalmente qualquer coisa, seja nulo, positivo ou negativo.
Passo 2
Então, como o simples é o belo, podemos simplesmente tomar definida em partes, sendo:
Agora, podemos desenhar o gráfico dessa função:
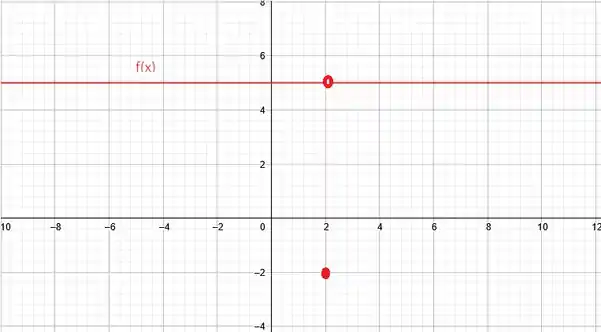
Resposta
Exercícios de Livros Relacionados
Para o limite x 3 + x + 1 = 3 , use um gráfico para determinar o valor do δ correspondente a ε = 0,4 .Usando um sistema de computação algébrica para resolver a equação x 3 + x + 1 = 3 + ε , determine
Demonstre cada afirmação usando a definição ε , δ de limite e ilustre com um diagrama como o da Figura 9. lim x → 1 2 x + 3 = 5
Demonstre cada afirmação usando a definição ε , δ de limite. lim x → 6 x 4 + 3 = 9 2
Para o limite: lim x → 0 e x - 1 x = 1 Ilustre a Definição 2 encontrando os valores de δ que correspondam a ε = 0,5 e ε = 0,1 .
Mostre por meio de um exemplo que lim x → a ��� f x + g ( x ) ��� pode existir mesmo que nem lim x → a f ( x ) nem lim x → a g ( x ) existam.