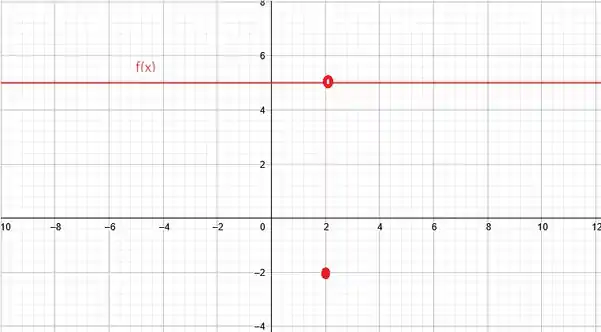
5b) Sabe-se que e é definida em Todas as afirmativas abaixo são falsas. Tente desenhar um contraexemplo para cada uma delas.
Passo 1
Vamos juntos matar essa questão!
Primeiro, vamos entender porque essa afirmação é falsa. Sabemos que:
Mas, é verdade que isso implica ?
Bom, para responder essa pergunta vamos antes relembrar o conceito de continuidade de uma função em um ponto do seu domínio:
é continua em
Logo, supondo que a resposta à nossa pergunta fosse “sim”, então teríamos:
Então, seria contínua em . Assim, estaríamos dizendo que se então é contínua nesse ponto. E isso, pelo próprio conceito que revisamos, não é verdade, pois existem funções que não são contínuas em , mas possuem limite, quando x tende a 2, iguais a 5. É por isso que a resposta à nossa pergunta é não e a afirmação feita, de fato, é falsa.
Passo 2
Agora que entendemos o porquê da afirmação ser falsa, vamos pensar em como construir um contraexemplo.
Como vimos no passo 1, a afirmação só seria verdadeira se for contínua em . Portanto, para desenharmos um contraexemplo, basta pensarmos em uma função que não seja contínua em , mas tenha . A ideia é pensar na função mais simples possível que obedece a:
Uma ótima opção é uma função definida por partes. Para que, com certeza, ela obedeça à primeira condição, podemos dizer que:
para todo
Já para satisfazer a segunda condição, basta definirmos que:
, quando
Assim, definimos como:
Passo 3
Agora, basta desenharmos o gráfico dessa função:
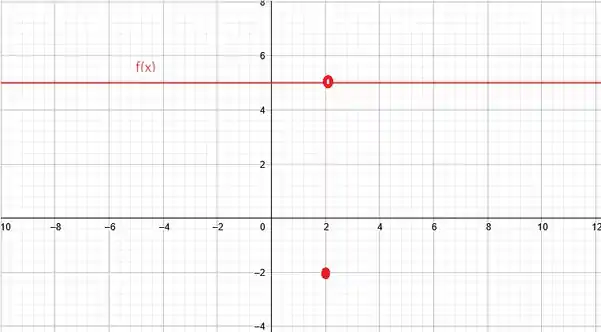
Resposta