UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 8
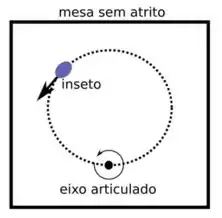
Um anel de raio e massa está deitado sobre uma mesa sem atrito. Ele é articulado por um eixo na sua borda. Um inseto de massa anda sobre o anel com uma velocidade constante relativo ao anel, e começando no eixo articulado, quando o anel está em repouso. Assuma o eixo para fora da página.
- Qual é a velocidade angular do anel quando o inseto está na metade da volta?
- Qual é a velocidade angular do anel quando o inseto está de volta ao eixo articulado?
Passo 1
Olá galerinha, tudo na paz com vocês?
Nessa questão temos um anel que está em cima de uma mesa plana, sem atrito, e que está articulado em um de seus pontos. Daí, um inseto audaz pousa em cima do anel justamente no ponto que está articulado, e começa a se mover com velocidade em cima do anel.
O enunciado nos pergunta qual a velocidade angular do anel em duas situações:
quando o inseto está na metade da volta;
quando o inseto concluiu a primeira volta.
Beleza?
Então galera, pra onde é que a gente vai nesse problema?!
O grande ponto é que, como não há torque externo, o momento angular se conserva.
Vocês lembram como calculamos o momento angular do inseto com relação ao eixo articulado?
onde é a distância do inseto, em cada instante, até o eixo articulado.
Além disso, temos também que calcular o momento angular do anel. Basicamente, ele vale:
Agora que já sabemos disso, vamos lá! Mãos à obra!
Passo 2
Bom, vamos começar calculando momento angular total no início do movimento:
Porém, o enunciado nos diz que inicialmente o anel está em repouso. Então:
Já para o momento angular do inseto, como inicialmente o inseto está em cima do eixo articulado, sua distância até o eixo é nula. Logo:
Sendo assim, encontramos que:
Massa! Esse momento angular precisa se conservar.
Passo 3
Vamos começar analisando quando o inseto está na metade da volta.
Se ele está na metade da volta, deve estar diametralmente oposto ao eixo articulado, ou seja:
Daí:
Beleza!
Já para o anel, temos:
Mas, qual o momento de inércia do anel, mesmo?
Basta fazermos:
Como no anel a distância de qualquer ponto é fixa e vale , temos que:
Show de bola! Logo, o momento angular total quando o inseto está na metade da volta, vale:
Pela conservação do momento angular total:
Excelente! Essa é a velocidade angular do anel na metade da volta do inseto!
Passo 4
Já quando o inseto completou a volta, ele vai estar novamente em cima do eixo articulado.
Assim, novamente teremos:
Logo:
Daí, substituindo na equação da conservação do momento angular:
Portanto, quando o inseto volta à posição inicial, o anel está novamente em repouso.
Ufaa! Terminamos!
Espero que vocês tenham entendido tudo bem direitinho!
Até a próxima 😊