Uma criança em um carrossel executa um movimento circular uniforme tal que no instante inicial sua velocidade em relação a um referencial cuja origem está no centro do carrossel. Se após sua velocidade é a aceleração centrípeta da criança vale:
(a)
(b)
(c)
(d)
(e)
Passo 1
Vamos desenhar, se liga:
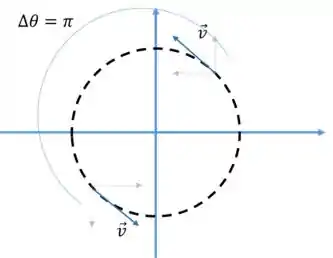
Percebe-se que, como a velocidade deve ser sempre tangencial à trajetória circular, com a mudança de sinais das componentes da velocidade nós percebemos que o deslocamento no intervalo foi de , logo:
Passo 2
Achamos a velocidade resultante da seguinte maneira:
Como o movimento é circular uniforme, a velocidade se mantém constante e, então:
Desta forma, usando a fórmula da aceleração centrípeta:
Resposta
(e)
Exercícios de Livros Relacionados
Uma partícula P se move com velocidade escalar constante sobre uma circunferência de raio r=3,00m (Fig. 4 56) e completa uma revolução a cada 20,0s . A partícula passa pelo ponto O no instante t= 0 .
Um astronauta é posto em rotação em uma centrífuga horizontal com um raio de 5,0m . (a) Qual é a velocidade escalar do astronauta se a aceleração centrípeta tem um módulo de 7,0g ? (b) Quantas revoluç
Um carrossel de um parque de diversões gira em torno de um eixo vertical com velocidade angular constante. Um homem em pé na borda do carrossel tem uma velocidade escalar constante de 3,66m / s e uma
Uma bolsa a 2,00m do centro e uma carteira a 3,00m do centro descrevem um movimento circular uniforme no piso de um carrossel. Os dois objetos estão na mesma linha radial. Em um certo instante, a acel
75. Nos Problemas de 74 a 76 são fornecidas algumas equações que devem ser usadas para resolver um problema. Para cada um deles, você deve a. Escrever um problema realista para o qual estas equações s