3. Ao passar pelo ponto mais baixo de um loop circular de uma montanha russa de raio , a força normal aplicada no passageiro de massa igual a pelo banco sobre o qual ele está sentado é igual a . Quanto vale a velocidade do passageiro nesse ponto?
Passo 1
Olá, pessoal! Tudo bom? Aqui nós temos uma loop de raio de uma montanha e queremos saber a velocidade do carrinho no ponto mais baixo do loop.
Então vamos começar desenhando essa situação destacando as forças que estão atuando ali.
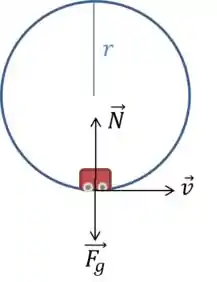
Onde temos a força gravitacional apontando para baixo, a força normal perpendicular ao carrinho e a velocidade tangenciando a circunferência aquele ponto.
Agora vamos relacioná-las!
Passo 2
De acordo com o movimento circular temos que
Onde é a força resultante do sistema, que faz com que o carrinho continue seu movimento e a é a nossa aceleração radial. Com isso, temos que
Ajeitando, temos que
Agora que já relacionamos as forças, vamos usar os dados do problema.
Passo 3
Temos pelo enunciado que
Substitundo na fórmula ficamos com,
Ajeitando,
Simplificando
Isolando
Prontinho!
Resposta
Letra C