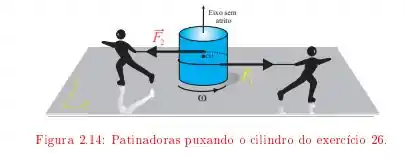
Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .
Quais são a aceleração angular e a velocidade angular em função do tempo?
Passo 1
Oiie, tudo bem?
Temos aqui um disco uniforme que é puxado por duas patinadoras como no esquema a seguir
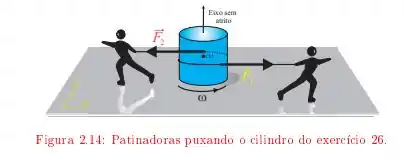
este disco tem uma massa e raio . Elas aplicam forças e de forma que o giro do disco é acelerado por ambas as forças durante , o objetivo desta alternativa é
Quais são a aceleração angular e a velocidade angular em função do tempo?
A aceleração angular pode ser obtida através da relação
e, tendo em vista que as forças são constantes, temos que a velocidade poderá ser obtida em termos da aceleração angular diretamente! Saca só!
Passo 2
Para obter o torque resultante devemos considerar o efeito de ambas as forças na rotação do cilindro! Note que da forma que elas são aplicadas, o efeito de ambas as forças se somam, de forma que o torque resultante será
pela definição de torque temos que
ou seja, temos que
analogamente, temos que
Ou seja, temos que o torque resultante é
Vamos usar isso para calcular a nossa aceleração angular!
Passo 3
Para calcular a nossa aceleração angular precisaremos de momentum de inércia de nosso cilindro, a expressão é dada por
obtendo então
Ou seja, temos que pela segunda lei de Newton das rotações, temos que
e, como esta aceleração é constante, temos que a velocidade angular é dada por
Essa alternativa foi isso! Te vejo na próxima! Até já!
Resposta
e