No dia 15/02/2013, um meteorito atingiu a cidade de Chelyabinsk, na Rússia, deixando em torno de 950 pessoas feridas, a maioria sem gravidade. Diversas imagens registradas por câmeras de monitoramento foram divulgadas pelas agências internacionais de notícias. Imediatamente cientistas da Agência Espacial Europeia utilizaram algumas dessas imagens em busca da localização de fragmentos do meteorito, descrevendo equações utilizadas no ajuste para localizar sua posição em função do tempo através de uma modelagem simples de movimento de projétil. Suponha que a equação de ajuste para a posição do meteorito (), determinada a partir de uma imagem adquirida por uma câmera de segurança de uma residência (), haja sido, em função do tempo, dada por:
Em um sistema de coordenadas onde os eixos e definem o plano horizontal e o eixo vertical.
a) Determine os vetores velocidade e aceleração do meteorito determinados pela câmera de segurança da residência, respectivamente descritos por , .
Suponha agora que esta mesma câmera de segurança () haja podido registar, na mesma imagem, a passagem de um automóvel () pela rua durante a queda do meteorito, fornecendo uma equação de ajuste para a posição do automóvel dada por:
b) Considerando que o tempo de queda do meteorito até a colisão com a Terra foi de aproximadamente 5 segundos, determine o deslocamento escalar total realizado pelo automóvel durante este tempo. (atenção: este ítem independe do )
c) Sabendo que o automóvel também possuía uma câmera e pôde registrar o movimento do meteorito, determine os vetores posição e velocidade do meteorito medidos por esta câmera, respectivamente descritos por , .
O próximo ítem é independente dos três anteriores:
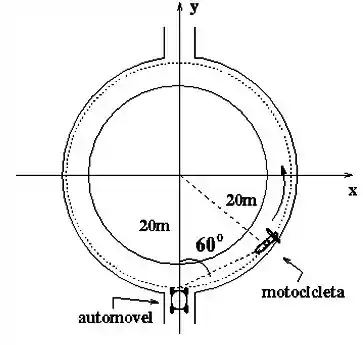
d) Considere agora que, instantes antes da queda do meteorito, o automóvel esteja parado aguardando para entrar em uma rotatória de 20 metros de raio. Ele observa uma motocicleta já contornando a curva e estima que, quando esta moto está a um ângulo de 60° à sua direita (veja figura), ela possui uma velocidade escalar de . Determine o vetor aceleração da motocicleta neste instante, escrevendo-o explicitamente em termos dos vetores unitários do sistema de referência apresentado.
Passo 1
(a)
Basta lembrar que:
E analogamente:
Passo 2
(b)
Dado:
Basta calcular a posição nos instantes:
Inicial:
Final:
Agora para achar o deslocamento, é só encontrar a variação:
Passo 3
(c)
Obtemos pela fórmula do movimento relativo:
Para encontrar a velocidade, basta derivar:
Passo 4
(d)
A bicicleta descreve um movimento circular uniforme, a aceleração é centrípeta (direção radial), dada por:
O triângulo mostrado é equilátero e assim o vetor aceleração faz um ângulo de 30° com o sentido negativo do eixo . Em termos dos vetores unitários de base e portanto:
Resposta
(a)
(b)
(c)
(d)