Sabemos que o comprimento de um círculo é dado por (onde, é o comprimento, e é o raio da circunferência). Em cada período, o movimento circular uniforme executa (um) comprimento circular. A frequência é o inverso do período. Com essas informações você está preparado para resolver o exercício proposto.

Duas polias de raios e estão ligadas entre si por uma correia. Sendo e sabendo-se que a polia de raio efetua , a frequência da polia de raio , em , é:

(a)

(b)

(c)

(d)

(e)

(a)

Vamos desenhar esse sistema com polias e uma correia unindo elas:

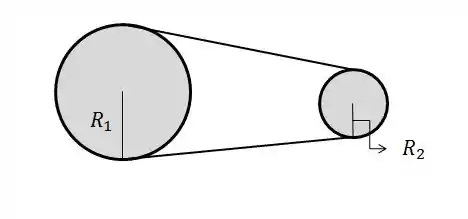
Como elas estão pressas por essa corrente, a gente pode dizer que a velocidade com que o fio dá a volta nelas é a mesma, já que só um fio.

Mas gente, esse é o tempo necessário para ele dar uma volta na circunferência. Esse é o nosso famoso Período

Mas naquelas informações que o enunciado fala pra gente ele diz que a frequência é o inverso do período, ou seja:

Assim:

Uhuuul! Conseguimos relacionar a velocidade com a frequência.! Fazendo a mesma coisa para a outra polia:

Como esses valores são iguais, porque elas são obrigadas a girar juntas:

Então:

Como , e :

Maravilha!!