UnB. Física 1. Lista 4: Movimento em Duas e Três Dimensões. Questão 8b.
Um modelo de rotor de helicóptero tem 4 lâminas, cada uma com de comprimento, do eixo central à ponta. A frequência de rotação do rotor dentro do túnel de vento é de .
(b) Determine a aceleração radial da ponta da lâmina, expresse como múltiplo da aceleração da gravidade, .
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nessa questão temos um helicóptero cujo rotor tem 4 lâminas, cada uma com o comprimento de .
No item anterior, vimos que a velocidade linear da ponta da lâmina é de .
Com essas informações, vamos em busca de descobrir a aceleração radial da ponta da lâmina.
Ta certo? Então como fazemos isso?? 🤔🤔
A aceleração radial ou também a aceleração centrípeta é a aceleração que um corpo sente em direção ao centro de rotação do movimento.
Assim como podemos exemplificar em
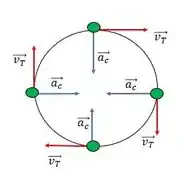
Entendeu? 😉
Passo 2
Mas então como calculamos essa aceleração.
Temos duas formulinhas que podemos usar
Como já calculamos (velocidade linear) anteriormente, podemos usar a primeira
Se e , logo
No enunciado, foi pedido para expressar o resultado em função da gravidade .
Considerando como
Lembra nas corridas de Formula 1? Onde tal piloto sente uma aceleração de em uma curva?
Então, nesse caso, se tivesse alguém preso na ponta da lâmina do helicóptero, a aceleração que seria sentida seria de . Muita coisa, não é? 👀👀
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
