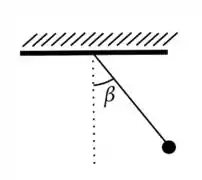
3) Uma partícula de massa está presa a um fio ideal de comprimento cuja outra extremidade está fixada ao teto. Largada do repouso, a partícula faz um ângulo com a vertical como indica a figura. O módulo da velocidade da partícula no momento que chega ao ponto mais baixo é:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, galerinha!! Esse é um problema de conservação da energia mecânica. Nós temos dois pontos para comparar. O ponto demonstrado na figura, onde a partícula está em repouso e o ponto mais baixo onde a partícula possui velocidade :
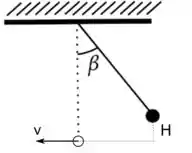
Dessa maneira, podemos adotar o ponto mais baixo como o ponto de energia gravitacional igual a zero. Então a ideia usar a conservação da energia mecânica para poder encontrar essa velocidade :
Manipulando um pouco essa expressão temos que:
O que falta é a gente escrever quem é esse em função do que a gente já tem... Vamos lá então!!
Passo 2
Podemos representar os dois pontos com essa figura aqui:
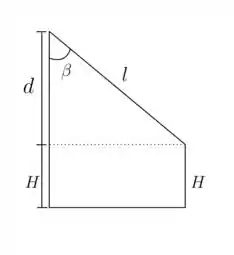
No triangulo retângulo podemos usar uma o cosseno daquele ângulo para encontrar aquele :
Mas como aquela reta corresponde o comprimento do fio quando a partícula está no ponto mais baixo, temos:
Então, usando a equação que obtemos no passo anterior temos:
E aí resolvemos essa😊 Vamos para a próxima??
Resposta
(d)