Uma roda-gigante com 10,0 de raio faz uma revolução a cada 24 . Ao chegar à parte mais alta do percurso, praticamente a um diâmetro de distância do solo, um passageiro deixa cair uma pedra. A que distância do ponto do solo diretamente abaixo do centro da roda-gigante cai a pedra? Utilize se necessário =3.
a) 0
b) 1,0 m
c) 5,0 m
d) 6,1 m
e) 10,0 m
Passo 1
Então, bora dar uma volta nessa roda gigante aí:
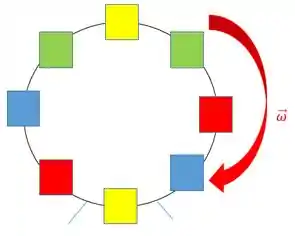
Onde essa velocidade angular pode ser encontrada:
Só que ali, no vagão mais alto, largou-se uma pedra.
Para saber qual distância a pedra irá alcançar, é preciso conhecer a velocidade com que ela é largada.
Passo 2
Imediatamente antes de largar a pedra, você concorda comigo que a pedra estava rotacionando junto com a roda gigante, isso é, a pedra possuía a mesma velocidade angular que a roda gigante.
A partir dessa velocidade angular, podemos calcular a velocidade linear da pedra:
Quando se larga a pedra, essa velocidade linear que ela tinha, fará com que ela alcance uma distância antes de chegar ao solo.
Passo 3
Agora começa um lançamento de projétil:

O projétil começa o seu percurso com uma altura igual ao diâmetro da roda gigante ().
Analisando o movimento:
Em y:
Em x:
Resposta
Letra c)