A figura a seguir mostra um objeto uniforme que rola sem deslizar sobre um plano inclinado. O objeto possui massa , raio e momento de inércia ao redor do eixo de rotação. Sabe-se que quando o objeto é liberado do repouso a partir de uma certa altura , ele é lançado horizontalmente ao chegar à base do plano inclinado, tocando o solo a uma distância horizontal do ponto de lançamento.
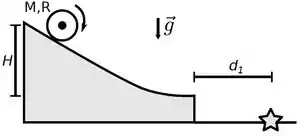
Na iminência do lançamento horizontal o centro de massa do cilindro possui uma velocidade . Sabendo que o , qual é o período de rotação do cilindro em torno de seu centro de massa?
Dado: considere
Passo 1
Sabendo a velocidade translacional e o raio do cilindro, podemos calcular a sua velocidade angular
Agora basta lembrarmos a relação entre a velocidade angular e o período de rotação
Lembrando que
Resposta
(D)