1) Um carro descreve um movimento circular uniforma com velocidade de módulo constante em uma pista circular de raio , ilustrada na figura abaixo. Qual o módulo da aceleração média , no deslocamento do ponto ao ponto ?
a)
b)
c)
d)
e)
Passo 1
Fala aí, galerinha!! Nesse problema a gente se depara com um caso de movimento circular uniforme. A ideia é avaliar o movimento em dois pontos e da figura dada e calcular a aceleração média entre esses pontos. Para isso, a gente lembra que a aceleração média é dada por:
Onde é a velocidade no ponto e é a velocidade no ponto . Por ser uma grandeza vetorial, é legal a gente representar as velocidades e tomar cuidado com a forma vetorial delas, beleza? Então vamos lá!
Passo 2
Bom, o problema nos disse que é um movimento circular uniforme, então em cada ponto a velocidade vai ter o mesmo módulo... mas cuidado! O módulo é sempre o mesmo, mas o vetor é sempre diferente. Olha só como ficam representados os vetores velocidade nos pontos dados:
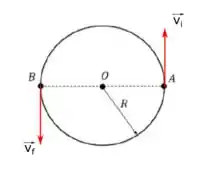
Então a gente percebe que os vetores e possuem o mesmo módulo mas possuem sentidos opostos. Por esse motivo a gente pode escrever o seguinte:
Dessa maneira, a aceleração média fica:
O exercício nos pede o módulo da aceleração, então fazemos:
Como sabemos que a velocidade sempre tem o módulo dado por temos:
Beleza!! Só tá faltando saber quem é aquele ali!
Passo 3
Nós temos uma meia volta de um movimento circular, certo? Podemos relacionar esse intervalo de tempo com a metade do tempo que demoraria para esse carro dar uma volta completa, ou seja, com o período do movimento circular .O período de um movimento circular uniforme de velocidade e raio é dado por:
Então temos:
Usando esse intervalo na aceleração, temos:
E aí resolvemos essa 😊 Vamos para a próxima??
Resposta
a)