UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 3
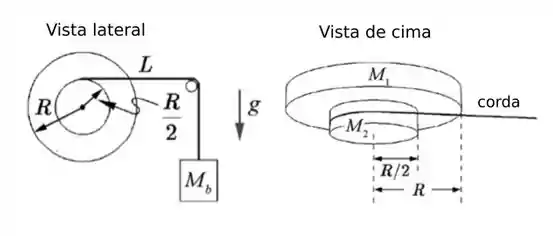
Considere uma roda fixa que consiste de um disco cilíndrico uniforme de raio e massa e um segundo disco cilíndrico uniforme de raio e massa que está encaixado concentricamente ao primeiro disco. A roda gira livre de atrito em torno do eixo central. Uma corda é enrolada em torno do disco menor. A ponta livre é atada a um bloco de massa de tal forma que os dois discos girem enquanto o bloco desce. A aceleração da gravidade tem magnitude . O bloco é solto do repouso. Qual o tempo para o bloco cair de uma distância ? Dê sua resposta em função das variáveis do problema.
Passo 1
Faaaaala gente bonita do Responde Aí, tudo certinho com vocês?
Nessa questão temos um problema bem interessante sobre rodas, fios e bloquinhos (a cara da mecânica né? Haha). Pois então, basicamente temos duas rodas concêntricas (seus centros estão alinhados) e que estão fixas uma na outra (rodam juntas).
Daí, é amarrado um fio em torno da roda menor e é preso um bloco de massa na outra ponta do fio. Naturalmente, a querida gravidade vai fazer o bloquinho descer, e as rodas começarem a girar, certo?
A pergunta do problema é quanto tempo o bloquinho demora pra cair uma distância .
Sacaram?!
Nesses problemas o ponto crucial é conseguir determinar a aceleração do sistema. Depois de encontrar a aceleração é só usar a equação horária do MRUV (movimento com aceleração constante) e determinar o tempo pedido. Mas, como determinamos a aceleração?
Então galera, a ideia principal é usarmos a equação que persegue esses problemas de dinâmica envolvendo rodas, discos, pneus, e tudo aquilo que gira haha.
onde é o torque atuante nas rodas, o seu momento de inércia, e a aceleração angular.
Daí, a partir da aceleração angular podemos usar que:
Massa! Agora que já sabemos disso, vamos lá! Mãos à obra 😊
Passo 2
Bom, pra começar, vamos analisar a equação:
O torque envolvido, como podemos ver na figura abaixo, é justamente o associado à força peso atuante no bloquinho.
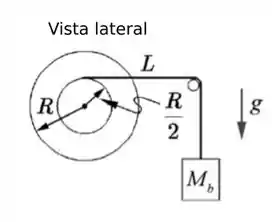
Assim, temos:
Massa! Olhando agora para o lado direito da equação, precisamos determinar o momento de inércia associado. Lembra quanto vale o momento de inércia de um disco de massa e raio ?
Vale:
Aqui, temos dois discos que giram juntos com aceleração angular logo:
Onde e são os momentos de inércia dos dois discos. Logo:
Daí, substituindo na nossa equação vamos encontrar:
Portanto:
Excelente!
Passo 3
Agora que já calculamos a aceleração angular, podemos usar que:
E calcular a aceleração linear. Pelo vínculo geométrico do fio, que é inextensível, a aceleração linear de um ponto do disco menor, é igual à aceleração linear do fio, que é igual à aceleração linear do bloquinho. Logo:
Ou seja:
Agora que já temos a aceleração, podemos substituir na equação horário do MRUV, a famosa equação do sorvetão haha!
Temos para o nosso problema que:
pois o bloco saiu do repouso.
Então:
Substituindo , temos:
Prontinho!!!
Curtiram a solução? Responde Aí!