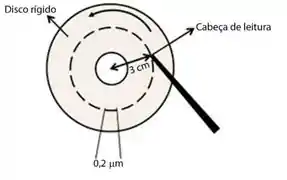
Considere um computador que armazena informações em um disco rígido que gira a uma frequência de 120 Hz. Cada unidade de informação ocupa um comprimento físico de 0,2μm na direção do movimento de rotação do disco. Quantas informações magnéticas passam, por segundo, pela cabeça de leitura, se ela estiver posicionada a 3 cm do centro de seu eixo, como mostra o esquema simplificado apresentado abaixo? (Considere π ≈ 3.)
a)
b)
c)
d)
Passo 1
A gente precisa encontrar o número de informações magnéticas que passam por segundo pela cabeça de leitura do disco rígido. Pra fazer isso a gente vai primeiro encontrar a velocidade angular
Usando a relação de velocidade linear com velocidade angular, temos:
Mas podemos calcular a velocidade angular também, né? Usando que:
Substituindo os valores na equação temos:
Passo 2
Para encontrarmos a distância percorrida nessa velocidade em 1 segundo, é só usarmos a formulinha de velocidade angular constante:
E agora pra encontrar o espaço percorrido é só a gente fazer:
Onde é a distância entre o centro do disco e a cabeça de leitura e vale . Assim temos, aproximando como recomenda o enunciado.
Sabemos que uma unidade de informação magnética que chamaremos de ocupa , vamos converter esse comprimento para metros fazendo:
Assim uma unidade de informação ocupa um espaço de , como temos , só usarmos uma regrinha de três! Então temos:
Portanto, em um segundo, passam unidade de informações magnéticas pelo equipamento de leitura.
Showww!
Resposta
d)