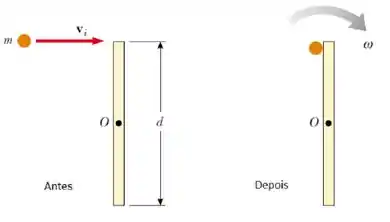
Um projétil de massa se move para direita com velocidade conforme figura ao lado. O projétil atinge e adere à extremidade de uma barra de massa , comprimento , que pode rotacionar em torno de um eixo que passa pelo centro. (a) Encontre a velocidade angular do sistema logo após a colisão. (b) Determine a perda de energia mecânica devido à colisão.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma bolinha (projétil) que colide com uma barra e faz ela rotacionar em torno de um eixo. E ele pede pra gente determinar a velocidade angular e a perda de energia mecânica do sistema depois da colisão.
Vamos começar tratando o projeto e a barra como um sistema isolado, que não experimenta torque externo. Então, nosso momento angular é conservado:
Como o momento angular pode ser dado pelo produto entre o momento de inércia e a velocidade angular , vamos usar essa relação para encontrar a velocidade angular do sistema.
Em seguida, vamos usar a velocidade angular para encontrar a variação de energia mecânica do sistema, que é apenas cinética após a colisão.
Vamos lá!
Passo 2
O momento angular inicial do sistema é dado pelo momento angular da partícula mais o momento angular da barra:
Onde e são a massa e velocidade da partícula, respectivamente.
O nosso momento angular final vai ser dado pelo produto entre o momento de inércia e a velocidade angular :
O momento de inércia total, , é dado pelo momento de inércia da barra retangular mais o momento de inércia da partícula:
Onde é a massa da barra e comprimento da barra.
Passo 3
Com essas equações em mãos, nós conseguimos usar a relação:
Substituindo o momento de inércia e o momento angular inicial:
Isolando :
E encontramos nossa velocidade angular.
Passo 4
Repare que agora ele pede a perda de energia mecânica devido à colisão. Essa energia vai ser igual a variação de energia cinética:
Nossa energia cinética inicial é dada por:
Porque temos apenas o movimento da partícula. Após a colisão, temos uma energia cinética rotacional, que é dada pela fórmula:
No passo anterior, nós encontramos e . Substituindo os resultados que encontramos:
Então, nossa variação de energia será:
Prontinho, galera! Até a próxima! 😉