Em um movimento circular uniforme onde os vetores posição, velocidade e aceleração da partícula valem e , respectivamente, (considere a origem do sistema de referência no centro do círculo) marque a alternativa correta para o resultado das seguintes equações:
, e /()
A. , respectivamente;
B. , respectivamente;
C. , respectivamente;
D. . , respectivamente;
E. , respectivamente;
Passo 1
Vamos desenhar uma partícula numa trajetória circular em movimento uniforme.
Como é uniforme, só teremos a aceleração centrípeta, ela não muda o valor da velocidade só uda a direção e o sentido, isso é o que permite a partícula rodar.
A velocidade escalar é tangente a trajetória.
E o vetor posição, vai da origem até a partícula.
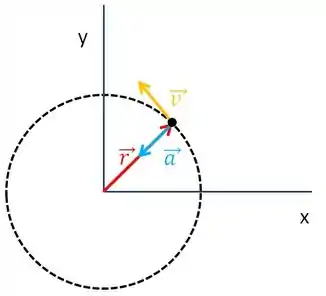
Outra coisa importante a se notar:
Qual é o ângulo entre e ?
Isso ve lá da geometria plana. Que fala pra gente que se temos uma reta tangente a circunferência em um certo ponto P, então o ângulo entre a reta tangente e o raio que vai do centro até esse ponto P é .
Então o ângulo entre e é.
Maravilha, vamos resolver aquelas contas.
Passo 2
A primeira conta que ele fala pra gente é:
Só escrevi a definição de produto escalar, ok?
E lembrando que esse é o ângulo entre e .
Olhando pra figura,
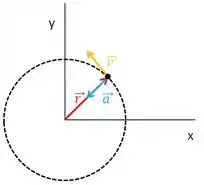
e para o que a gente discutiu no passo 1, temos que:
Beleza, a primeria conta dá .
Passo 3
A segunda conta que ele fala pra gente é:
Agora o é o ângulo entre e .
Olhando pra figura:
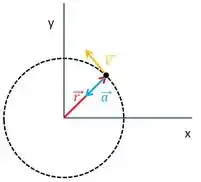
temos que as setas da posição e da aceleração estão em sentidos opostos, ou seja, o ângulo entre elas é :
Beleza, a segunda conta dá .
Passo 4
A terceira conta que ele fala pra gente é:
Agora o é o ângulo entre e .
Olhando pra figura:
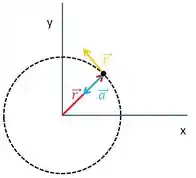
temos o mesmo esquema da primeira conta já que a aceleração e a posição estão na mesma direção (em sentidos opostos), ou seja, o ângulo entre e é 9:
Beleza, a terceira conta dá .
Então ficamos com:
Resposta
Alternativa B