UNB, Sem Campus, Física 1, Provas Mecânica Clássica - 2022.2, Questão 2.
2. Um projétil de massa é lançado com uma velocidade horizontalmente e na direção norte a partir de uma posição de colatitude . Determine a direção e a magnitude da força de Coriolis em termos de , , e da velocidade angular da Terra . Como a força de Coriolis se compara ao peso do projétil se e ?
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema queremos obter a direção e a magnitude da força de Coriolis em função de , , e (velocidade angular da terra).
Lembra como podemos fazer isso? 🤔
A força de Coriolis é dada pela fórmula
No caso, é a velocidade angular da terra .
No enunciado foi dito que o disparo foi dado horizontalmente para o norte. Isso significa que e fazem um ângulo de entre si.
Vale observar também que na verdade é pois a partir do ângulo em relação ao centro do planeta a força é diferente...
Com essas informações podemos começar nosso probleminha! 😁
Passo 2
Se e são e , respectivamente, a força de Coriolis é dada por
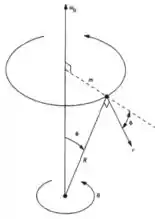
E também como e são perpendiculares e aponta para o norte, a força de Coriolis deve apontar para o oeste e ter modulo
Para e , temos que
Queremos obter a relação entre a força e a massa do projetil, então vamos isolar em um lado da igualdade...
Com isso, vemos que a força equivale a multiplicado pela velocidade angular da terra ao comparar com a massa do projetil!
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
