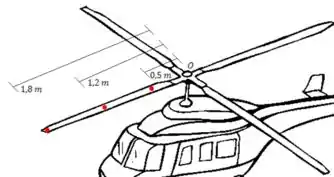
Um helicóptero que está se preparando para decolar, liga suas hélices. Nesse momento a hélice possui velocidade constante, realizando uma volta completa em . Determine a velocidade angular das pás do helicóptero e o deslocamento em cada ponto marcado em vermelho, mostrado no desenho abaixo, após 4 segundos.
Passo 1
Vamos começar achando a velocidade angular, como a velocidade é constante a velocidade angular deve ser constante também. A fórmula da velocidade angular é
Ele deu o tempo que ele demora para dar uma volta, isso quer dizer que
E o período do movimento é
Resultando em
A unidade de velocidade deve ser sempre em radianos por segundo. Cuidado que o ângulo deve estar em radianos, e não em grau.

Passo 2
Como a velocidade angular é constante, podemos descobrir o deslocamento angular multiplicando a velocidade pelo tempo total do movimento que é .
O deslocamento pode ser relacionado com o deslocamento angular com
Então
Passo 3
Vamos fazer essa conta para cada ponto