UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 4 - Rotação, rolamento e corpos rígidos, Questão 9
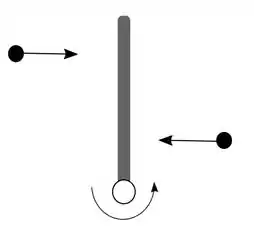
Uma haste rígida e uniforme de comprimento e massa está deitada sobre uma mesa sem atrito e é articulada por um eixo no ponto em uma de suas extremidades. Um objeto pontual de massa está movendo para direita com velocidade . Ele colide e gruda na haste a uma distância do eixo articulado. Um segundo objeto pontual também de massa movendo para a esquerda também atinge e gruda na haste no mesmo instante que o primeiro objeto, mas a uma distância . O momento de inércia da hasta para um eixo que passa pelo seu centro de massa e paralelo ao eixo articulado é . Depois da colisão o sistema rotacional sobre o eixo articulado está com velocidade angular .
- Qual é a velocidade angular ?
- Qual é a razão entre a energia cinética inicial e final do sistema ?
Passo 1
Eaí pessoal, como vocês estão?
Temos aqui um probleminha envolvendo colisão, momento angular, momento de inércia, vários conceitos legais pra gente trabalhar 😊.
Basicamente, dois objetos pontuais colidem com uma barrinha que estava inicialmente parada. Um deles colide a uma distância e outro a uma distância da extremidade articulada da barra. Após a colisão, esses objetos grudam na barrinha formando um único corpo, que passa a rotacionar em volta da articulação com velocidade angular .
O objetivo do enunciado é que determinemos , e também a razão entre a energia cinética final e inicial do sistema.
Pra fazer isso precisamos usar o conceito da conservação do momento angular, como não há torque externo ao sistema composto pela barra e pelos dois corpos, podemos afirmar que o momento angular total se conserva. Assim, nossa estratégia vai ser calcular o momento angular antes e após a colisão, para encontrar as informações pedidas, beleza?
Vamo nessa!
Passo 2
Então galera, vamos começar calculando o momento angular total logo antes da colisão.
Quanto aos objetos pontuais, que chamaremos de e , os seus momentos angulares com relação ao eixo articulado, vale:
onde é a distância do objeto até o eixo articulado.
Assim:
O sinal de negativo é porque o sentido de rotação é oposto ao de .
Massa! Já para a barra temos que inicialmente ela está em repouso, assim:
Portanto, o momento angular total inicial, vale:
Logo:
Perfeito pessoal 😊
Passo 3
Agora vamos calcular o momento angular imediatamente após a colisão.
Temos que os corpos estarão grudados na barra, e estarão rotacionando junto com elas, ou seja, com velocidade angular .
Como:
Teremos que:
Já para a barrinha, temos que:
Mas, esse é o momento de inércia em relação ao eixo articulado da barra, e no enunciado recebemos apenas o momento de inércia com relação ao centro de massa da barra.
Podemos então usar o teorema dos eixos paralelos:
onde é momento de inércia com relação ao eixo de interesse, o momento de inércia em relação ao CM e a distância entre os eixos.
Daí:
Excelente!
Substituindo na nossa expressão principal, vamos ter:
Juntando tudo:
Mas, pela conservação do momento angular, temos que:
Assim:
Aí sim! A primeira pergunta já foi 😊
Passo 4
A próxima parte é calcular a razão entre a energia cinética final e inicial:
Vamos começar calculando :
Mas a barra estava em repouso e . Assim:
Já após a colisão, a energia cinética final pode ser calculada considerando que:
onde é a distância até o eixo articulado. E, para a barra, podemos usar o centro de massa e tomar a distância entre o CM e o eixo articulado. Daí:
Vamos agora calcular a razão:
Substituindo os valores encontrados, temos que:
Mas, vimos no item anterior que:
Logo:
Portanto:
Aeee! Terminamos!
Curtiram a solução? Responde Aí!