(Capítulo 9.1 – Exercício 37) A fita em um videocassete VHS padrão tem um comprimento total de , o suficiente para operar durante . Quando no início, o carretel cheio tem um raio externo de e um raio interno de . Em algum momento da operação, os dois carretéis têm a mesma rapidez angular. Calcule esta rapidez angular em radianos por segundo e em revoluções por minutos. Dica: Entre os dois carretéis, a fita corre com rapidez constante.

Passo 1
Oii gente, a fita VHS não é algo que a gente ta tããão habituado a ver, mas vamos aplicar a física nela ok? Hahahaha
Aqui o que a gente tem que perceber é o seguinte: como , as duas fitas vão ter a mesma velocidade angular e tangencial quando os raios forem iguais!
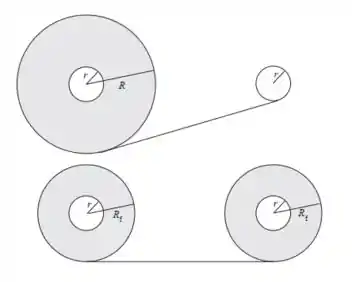
A segunda coisa que temos que perceber é que nas duas situações a quantidade de fita é a mesma, já que ela desenrolou de um lado e foi pro outro. Então as áreas das fitas também têm que ser iguais.
Passo 2
Passo 3
Então vamos lá! A velocidade angular é:
Essa velocidade pode ser calculada em função do comprimento da fita e do tempo que demorou pra ela rodar, ou seja:
Daí,
Passo 4
Agora vamos olhar para aquela brincadeira das áreas:
A área de fita no começo é igual a , e no final ela vai ser . Esse fator aparece porque são dois carretéis.
Juntando com a outra equação:
Passo 5
Agora é só substituir os valores numéricos, sem esquecer de ajeitar as unidades, como hora para segundo e milímetro para metro.
Ou, em revoluções por minuto:
Ihhh arrasamos!