Uma partícula descreve um movimento circular uniforme de raio em um plano horizontal, em um sistema de coordenadas onde a origem se encontra no centro da circunferência. Qual destas afirmações é falsa:
- A velocidade média depois de um período completo é nula
- A velocidade escalar média depois de um período completo é igual a
- O produto escalar entre o vetor velocidade e o vetor posição da partícula é sempre nulo.
- O produto escalar entre o vetor velocidade e o vetor aceleração da partícula é sempre nulo.
- O produto escalar entre o vetor aceleração e o vetor posição da partícula é sempre nulo.
Passo 1
Vamos analisar as alternativas uma a uma.
Alternativa (a) – Verdadeira.
A velocidade média a que o enunciado se refere é o vetor velocidade média que tem a fórmula:
Portanto, após um ciclo completo, o deslocamento vetorial é nulo, pois o ponto inicial e final do vetor são os mesmos. Então a velocidade média vetorial também será nula.
Passo 2
Alternativa (b) – Verdadeira.
O deslocamento escalar total é o comprimento do círculo, ou seja, . Então após um período completo T, teremos:
Passo 3
Alternativa (c) – Verdadeira.
Estando a origem do sistema de coordenadas no centro da trajetória circular, o vetor posição é sempre radial e perpendicular ao vetor velocidade instantânea, que é sempre tangencial à trajetória;
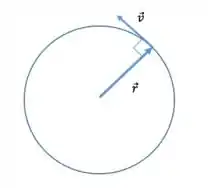
Passo 4
Alternativa (d) – Verdadeira.
Como o movimento é uniforme, não possui aceleração tangencial, apenas aceleração centrípeta. Logo, o vetor aceleração é radial, assim como o vetor posição. É, portanto, perpendicular ao vetor velocidade instantânea em todos os momentos.
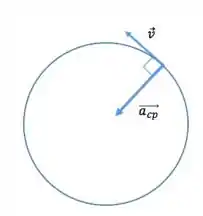
Passo 5
Alternativa (e) – Falsa.
Os vetores aceleração e posição apontam na mesma direção, mas em sentidos opostos. O único jeito do produto escalar ser nulo é se um dos vetores for nulo ou se eles forem perpendiculares. Como isso não ocorre, essa afirmativa é falsa.
Resposta
Letra (e)