Um carro de corrida efetua uma trajetória em um circuito circular de diâmetro igual a com módulo de velocidade constante igual a . O período do movimento é:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, pessoal!!
Nessa questão ele quer saber o período de um movimento circular!
O período é o tempo necessário que o carrinho demora para completar uma volta na circunferência, ou seja, percorrer .
Então, para uma volta:
O diâmetro da circunferência é o dobro do raio, então:
Então a distância percorrida é
Passo 2
A velocidade dada não está nas unidades do SI, então temos que converter de para :
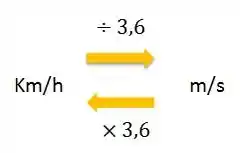
Então a velocidade em :
Maravilha!!
Passo 3
Agora é só calcular o período:
Show??!

Resposta
Alternativa (D)