USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 58a
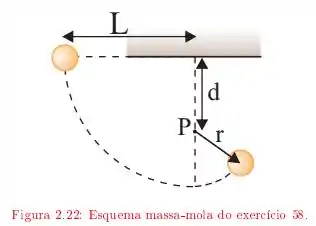
A corda da figura tem comprimento e a distância até o pino fixo é de . A bola é liberada, a partir do repouso, com a corda na posição horizontal, descrevendo a trajetória indicada pela linha tracejada como mostra a figura. Qual é a velocidade da bola:
quanto está passando pelo ponto mais baixo da trajetória?
Passo 1
Ooi gente, como vocês estão?
Nessa questão temos uma bolinha que está presa a um fio de comprimento . Ela é largada da posição horizontal, conforme mostrado na figura, e realiza uma trajetória circular até que o seu fio encontra o ponto .
Nesse momento a bola começa a girar em torno desse ponto .
Nesse item precisamos determinar a velocidade da bolinha quando ela passa pelo ponto mais baixo da sua trajetória, tranquilo?
Para fazer isso vamos utilizar a conservação da energia mecânica do sistema, já que na bola não age nenhuma força não-conservativa.
Vem comigo!!
Passo 2
A energia mecânica do sistema é composta pela parcela da energia cinética e da energia potencial gravitacional.
Assim, conservando a energia entre o momento inicial, em que a bola é largada do ponto mais alto da trajetória, até o momento em que ela atinge o ponto mais baixo, temos:
Daí:
Assim, como a diferença de altura entre os pontos mais alto e mais baixo da trajetória é justamente o negativo (já que a altura final é a menor) do comprimento da corda, isto é: . E, também, como no ponto inicial a bola é largada (ou seja, ), vem:
Substituido:
Excelente pessoal! Com isso matamos esse item 😊
Até a próxima!!