Um disco de raio gira em torno do seu centro com período de rotação igual a , como ilustrado na figura. Considere que a figura representa o disco em .
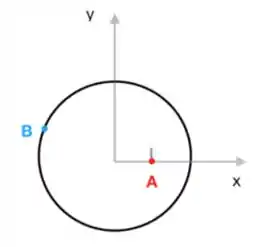
a) Calcule a aceleração centrípeta do ponto A.
b) Forneça a posição do ponto A em .
c) Determine a velocidade escalar e angular do ponto B em .
d) Numa mesma figura, faça o gráfico de dos pontos A e B no intervalo de tempo .
Passo 1
Fala galerinha, beleza? Partiu resolver esse problema sobre movimento circular!
O enunciado não deixou claro, mas a única coisa razoável que podemos tirar é que o disco executa um movimento circular uniforme de período . Com isso, podemos calcular a velocidade angular do disco:
Vamos supor também que a distância do ponto A ao centro do disco é . A aceleração centrípeta desse ponto será
Passo 2
Para resolver o item (b), vamos escrever as coordenadas e do ponto A em função do tempo. Quando o ângulo do ponto A com relação ao eixo for , temos que
Como o movimento é uniforme, temos
O ponto A parte do eixo com , de modo que :
Assim,
No instante , temos
Logo,
Como , segue que
Passo 3
No item (c), queremos achar as velocidades escalar e angular do ponto B. A velocidade angular é uma propriedade que independe da posição e como foi calculado no passo 1:
Para a velocidade angular:
Passo 4
A aceleração do ponto A já foi calculada no item (a):
Para o ponto B, temos
Essas acelerações são constantes no tempo de modo que os gráficos são dados a seguir:
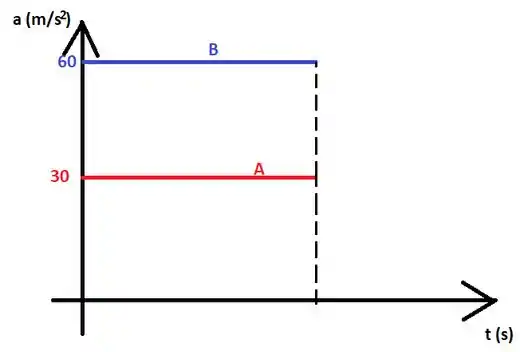
Com isso, finalizamos o problema 😉!