USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 61
Uma conta de massa enfiada em um aro circular de raio situado em um plano vertical, está presa por uma mola de constante de mola ao ponto , localizado no topo do aro. Na posição relaxada da mola, ela está localizada em , o qual é o ponto mais baixo do aro. Se soltarmos a conta, a partir do repouso, do ponto , que faz um ângulo de com , como indicado na figura , com que velocidade ela atinge o ponto ?
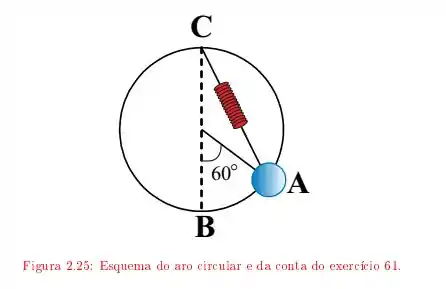
Passo 1
Fala aí pessoal, tudo tranquilo?
Nessa questão temos uma conta que pode rodar guiada por um aro. Essa mola está presa a uma mola, que está relaxada quando a mola está em .
Queremos soltar a conta do ponto e calcular a velocidade com que ela irá passar pelo ponto .
Para calcular essa velocidade, como a única força não dissipativa atuando é a normal (mas que é sempre perpendicular ao deslocamento da conta e por isso não realiza trabalho), podemos usar a conservação da energia mecânica entre os pontos e .
Vem com a gente que vai ficar bem clarinha a resolução 😊
Passo 2
Bom, a energia mecânica do sistema é composta por uma parcela de energia cinética e uma parcela de energia potencial. Ou seja:
Vamos começar escrevendo a energia mecânica para o ponto :
é altura que a conta se encontra no ponto . Vamos tomar como referência o nível do ponto . Ou seja, medimos a distância vertical entre e , isso é .
Já o da mola é o tanto que ela deformou em relação ao seu comprimento natural.
é a velocidade da conta no ponto , como a conta é largada desse ponto, temos que:
Vamos usar um ponto de geometria para calcular e .
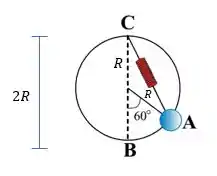
O comprimento natural da mola ocorre quando ela está alonga de até . Ou seja:
Vamos agora calcular o comprimento da mola quando ela está deformada de até , ou seja, vamos calcular .
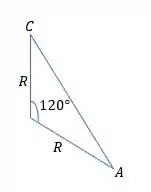
Usando a lei dos cossenos, temos:
Como:
Temos:
Excelente! Logo:
Pensando agora na altura , vamos ter:
Como:
Temos:
Logo, podemos finalmente escrever a energia mecânica do sistema em como:
Passo 3
Agora vamos escrever a energia mecânica do sistema em :
Como convencionamos o nível de referência da altura no próprio nível do ponto , temos:
Além disso, em o comprimento da mola é justamente o seu comprimento natural. Logo, ela não está deformada e temos:
Assim:
Excelente!
Como a energia mecânica se conserva, podemos igualar as duas expressões:
Daí:
Vamos substituir os dados do enunciado:
Daí, temos:
Logo:
Prontinhooo! Matamos mais uma questão 😊
Vocês curtiram? Responde Aí!