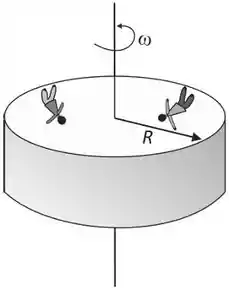
Uma estação espacial foi projetada com formato cilíndrico, de raio R igual a 100 m, como ilustra a figura abaixo. Para simular o efeito gravitacional e permitir que as pessoas caminhem na parte interna da casca cilíndrica, a estação gira em torno de seu eixo, com velocidade angular constante ω. As pessoas terão sensação de peso, como se estivessem na Terra, se a velocidade ω for de, aproximadamente,
a) 0,1 rad/s
b) 0,3 rad/s
c) 1 rad/s
d) 3 rad/s
e) 10 rad/s
Note e adote:
A aceleração gravitacional na superfície da Terra é g = 10 m/s2
Passo 1
Nesse problema o enunciado diz que a estação gira para simular o efeito gravitacional. Esse giro do cilindro vai gerar uma aceleração centrípeta e com ela uma força centrípeta, isso acontece na superfície terrestre também, onde a força centrípeta é igual ao peso do corpo.
Se liga da imagem onde o pontinho verde representa uma pessoa em cada ponto do cilindro com sua aceleração centrípeta e velocidade tangencial
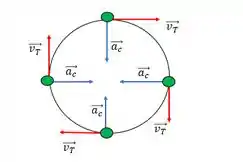
Pela segunda lei de newton temos o seguinte
Podemos então representar essa força no sentido da aceleração:

Passo 2
Como foi falado no passo 1, a força centrípeta que mantem a gente preso no movimento de rotação na terra é igual ao peso do corpo, e queremos com a rotação simular isso aqui, então faremos:
Cortando as massas dos dois lados temos:
Mas, como queremos saber da velocidade angular, devemos lembrar que:
Entããão, temos:
Como queremos a velocidade angular para qual a sensação de peso será igual a da terra, temos que a gravidade vale 10m/s2
Substituindo todos os dados na equação, temos que:
Show! Conseguimos!
Resposta
b) 0,3 rad/s