Um corpo de massa percorre, com velocidade angular constante , em sentido
anti-horário, uma trajetória circular de raio , cujo centro dista da origem do sistema de coordenadas , como mostra a figura.
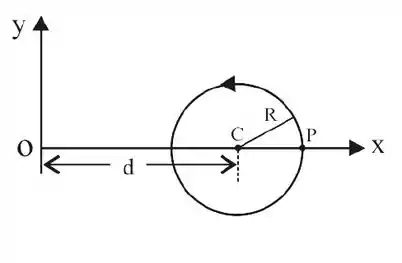
Sabendo que o corpo está passando pelo ponto no instante , a equação que descreve sua posição em relação à origem do sistema de coordenadas, em função do tempo , é dada por:
Os símbolos e representam vetores unitários, perpendiculares entre si, nas direções e sentidos dos eixos x e y, respectivamente.
Passo 1
Pra gente entender o que está acontecendo, vamos pensar que a trajetória tá centrada na origem. Considerando um instante qualquer, a posição que a partícula vai estar pode ser decomposta nas direções x e y
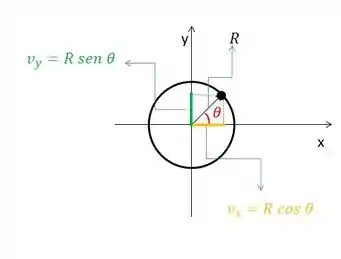
O que vai mudar quando a trajetória tá distante da origem vai ser só a componente da posição em x, pois a posiç em x está transladada de d, ou seja:
E em y fica tudo igual:
Show até aqui?
Então temos que o vetor posição é:
Mas a gente tem informação de ? Não!
Sabemos só que a velocidade angular é constante e vale . Então vamos usar a equação da posição angular em função do tempo, para um movimento uniforme:
Pois no inicio do movimento a partícula está sobre o ponto P, no eixo x.
Substituindo, temos:
Maravilha!