UFABC – Fenômenos Mecânicos – P3 – Questão 1
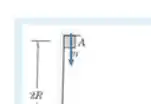
Um pequeno bloco de massa é liberado do repouso na posição deslizando ao longo da pista no plano vertical. Sabendo que a pista é lisa de até e rugosa em diante,
- Faça um diagrama de forças para o bloco nos pontos e .
- Quais são as forças normais exercidas pela pista sobre o bloco quando este passa pelas posições e ?
- Determine as velocidades do bloco nos pontos B e D
- Qual é a distância s percorrida pelo bloco ao longo da inclinação após passar pelo ponto D, até ele parar.
Use R=10m, 0.2, g=9,8
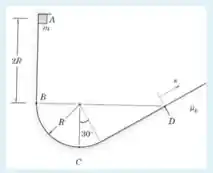
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas estou aqui para te ajudar! Vamos resolver juntos?
Letra a)
No ponto temos apenas a força peso (vertical para baixo, em azul):
No ponto B temos três: a força peso (segue sendo azul, apontando verticalmente pra baixo), a força normal que aponta sempre perpendicular à superfície e está representada em roxo. E a terceira é nossa novidade: a força centrípeta, pois temos o começo de um movimento circular. A força centrípeta aponta sempre pra dentro da trajetória. No nosso desenho ela está em vermelho.
Saca só:
No ponto C estamos no meio da trajetória circular, então temos a força centrípeta. Ela ainda é representada pela seta vermelha e aponta nesse ponto verticalmente para cima.
Temos também a força normal, que nesse ponto é vertical pra cima também. Ela é representada pela seta roxa.
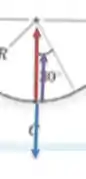
Beleza?
No ponto D temos que o bloco sai do movimento circular. Temos agindo sobre o bloco três forças: a força peso, sempre vertical pra baixo e está em azul. A força normal, que é perpendicular ao apoio, então nesse ponto é a seta em roxo. E a novidade é a força de atrito. Aqui ela está representada em verde. Ela aponta SEMPRE na direção OPOSTA ao movimento.
Daí o diagrama de forças nesse ponto é:
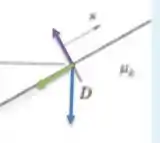
Passo 2
Letra b)
No ponto B a força Normal será igual a força centrípeta. Aqui você precisa lembrar que a força resultante em um movimento circular é igual a força centrípeta!
Como em B na direção horizontal só temos a força normal e a força centrípeta, então:
A força centrípeta é dada por:
A velocidade é a velocidade com que o corpo chega no ponto B. Ele parte do repouso, então por conservação de energia, podemos achar a velocidade em B se ele caiu uma altura de 2R:
Aí como a massa é , então a força normal é:
Já no ponto C temos que a força resultante é a diferença entre o peso do bloco e a normal:
A força peso é . Agora vamos determinar a força centrípeta.
Novamente vou usar a conservação de energia. Considerando que no ponto B tenhamos apenas energia cinética (vou considerar na linha horizontal do ponto B e velocidade é 20m/s) então a altura do ponto C é e podemos achar a energia cinética ali:
Assim a velocidade no ponto é . E daí podemos usar essa velocidade pra calcular a força normal:
Passo 3
Letra c)
As velocidades nos pontos e calculamos no passo anterior:
Passo 4
Letra d)
Como a pista é lisa até o ponto D, então quando ele chegar no ponto D ele vai ter a mesma velocidade do ponto B. Achamos .
Aí a energia cinética é totalmente convertida em energia dissipada pela força de atrito:
E a força de atrito é:
E como temos um plano inclinado, a normal é igual a componente vertical do peso (vetor pontilhado em azul):
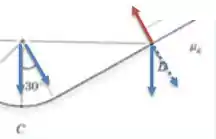
E essa componente pode ser escrita em termos do peso e do cosseno de pode ser escrita em termos do peso e do cosseno de :
E como , e podemos encontrar a distância que o bloco percorre até parar:
Pronto! A distância que o bloco percorre até parar é de
Resposta
