Uma bolsa a do centro e uma carteira a do centro descrevem um movimento circular uniforme no piso de um carrossel. Elas estão na mesma linha radial. Em um certo instante, a aceleração da bolsa é . Qual é a aceleração da carteira nesse instante, em termos dos vetores unitários.
Passo 1
Ele nos dá uma aceleração aí e nos diz que o movimento é circular uniforme. O que isso quer dizer?
Tudo! Movimento circular uniforme só tem aceleração centrípeta, então essa aceleração aí é a centrípeta
Vamos desenhar um esqueminha nesse do que está acontecendo nesse nosso carrossel verde abaixo, com a bolsa na cor preta e a carteira na cor roxa.
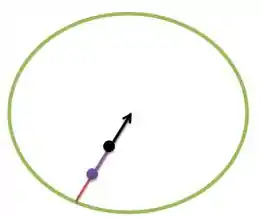
Passo 2
Sabemos que o módulo da aceleração centrípeta pode ser calculada por:
Mas para só pra pensar, se eles estão em cima do carrossel , eles estão sob mesma velocidade angular, pois a variação do ângulo num mesmo intervalo de tempo vai ser igual pra todos.
Sabemos também que e substituindo ali, teremos:
Passo 3
Escrevendo a aceleração de cada uma, teremos:
Dividindo uma pela outra, teremos:
E assim, teremos:
Passo 4
Beleza, mas quem é É justamente o módulo do vetor
Como calcula? Fácil!
Assim, será:
Passo 5
Beleza, já temos o módulo, mas queremos o vetor que representa a aceleração.
A gente sabe que ele deve apontar para a mesma direção que , porém com módulo . Pra achar esse vetor, temos que achar os vetores unitários que dão a direção para a aceleração da bolsa, pra fazer isto basta dividir o vetor pelo módulo do vetor.
Daí