
Passo 1
Bom, a primeira pergunta é sobre o trabalho realizado por uma força constante. Que que a gente vai usar aqui ?
Substituindo os valores que ele deu no enunciado a gente fica com isso aqui
Lembrando que ele pediu pra desenhar um diagrama com os vetores e
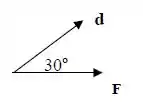
Passo 2
Letra b)
A idéia é a mesma que a questão de cima, só que agora vamos trabalhar com a força Peso
Fazendo já o diagrama que ele pediu pra ficar mais claro
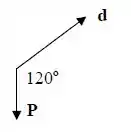
Substituindo os valores
Passo 3
Letra c)
Galera, geralmente o trabalho realizado pela força normal é zero, porque ele é perpendicular a trajetória, como esse caso aqui.
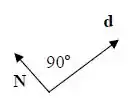
Como o ângulo é , o vai ser , zerando tudo.
Passo 4
Letra d)
Aqui vamos usar o teorema da energia cinética, que vai relacionar a energia com o trabalho realizado.
Como o bloco partiu do repouso, podemos considerar a energia cinética inicial .