Um bloco de massa é lançado em um plano inclinado, fazendo um ângulo com o solo, com velocidade inicial . Ele sobe, atinge o ponto mais alto da trajetória, e retorna à posição inicial. Considerando a aceleração gravitacional e o coeficiente de atrito cinético , responda às seguintes questões:
(a) Faça o diagrama de forças que atuam sobre o corpo no início do movimento.
(b) Descreva os valores das forças indicadas no item anterior em termo das variáveis do enunciado.
(c) Qual a distância total percorrida pelo corpo na subida?
(d) Qual o trabalho realizado pela força peso e pela força de atrito ao longo da subida.
(e) Qual o trabalho realizado pela força peso e pela força de atrito ao longo da descida.
(f) Qual a variação da energia cinética no trajeto total do corpo?
Passo 1
Temos um caso de um bloquinho no plano inclinado, o que é bem comum, né?
Porém, o bloquinho agora é lançado com uma velocidade , ou seja, ele vai subir a rampa até uma determinada altura e descer de volta. Lembrando que a superfície tem atrito.
Então, vambora resolver cada item.
Passo 2
(a) Faça o diagrama de forças que atuam sobre o corpo no início do movimento.
No momento inicial, o movimento do bloquinho é para cima da rampa, então a força de atrito vai estar para baixo na rampa (direção contrária).
Além disso, temos a força peso vertical para baixo e a força normal perpendicular à superfície do plano inclinado:
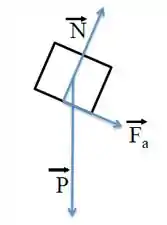
Passo 3
(b) Descreva os valores das forças indicadas no item anterior em termo das variáveis do enunciado.
Nós só podemos escrever as forças em função das variáveis . Além disso, os eixos do problema já estão definidos, sendo paralelo à rampa (para baixo) e normal à ela.
Começando com a força peso , vamos decompor ela em suas componentes:
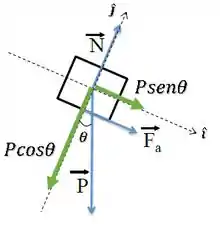
Assim, podemos dizer que a força peso será a soma de suas componentes nas direções dos eixos e :
Sabemos que a força , então:
Agora, vamos à força normal . Para escrevê-la em função das nossas variáveis, temos que relacioná-la com a componente da força peso na mesma direção.
Se temos um equilíbrio na direção , podemos dizer que:
Então, lembrando que ela está no sentido positivo do eixo, achamos que:
Por último, vamos à força de atrito , que aponta no sentido positivo de . Como o bloco está se movendo, a força de atrito é cinética, e tem a expressão:
Onde é o coeficiente de atrito cinético e é a força normal da superficie . Logo, temos que:
Passo 4
(c) Qual a distância total percorrida pelo corpo na subida?
A gente sabe a velocidade inicial e a aceleração, certo?
O bloquinho vai subir até que sua velocidade chegue a zero, então é só a gente usar aquelas equações de movimento uniformemente variado e achar qual a distância que ele chega até parar.
Já que não temos o tempo, é conveniente usar Torricelli:
Putzz, não pensei em usar Torricelli! Relaxa, dá pra achar o mesmo resultado por aquelas outras equações:
Mas voltando ao Torricelli, a velocidade final vai ser , a velocidade inicial vai ser o próprio , e o deslocamento vai ser a distância que queremos achar. Mas e a aceleração?
A aceleração, a gente acha pela segunda lei de Newton:
Lembrando aqui das nossas forças:
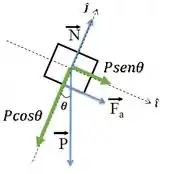
As forças em se anulam, então a força resultante será o somatório de forças em :
Cortando a massa dos dois lados, temos que a aceleração é:
Agora, é só substituir tudo isso no Torricelli, colocando sinais trocados entre a velocidade inicial e a aceleração (sentidos opostos):
A distância percorrida (em módulo) será:
Passo 5
(d) Qual o trabalho realizado pela força peso e pela força de atrito ao longo da subida.
Tanto a força peso quanto a força de atrito são constantes em todo o deslocamento, então podemos calcular o trabalho pelo produto da força com o deslocamento vezes o cosseno do ângulo entre eles:
Trabalho da força peso:
O trabalho da componente do peso em é nulo, pois apenas a componente da força na direção do deslocamento realiza trabalho. Então, usamos apenas a componente em :
Lembrando que o trabalho deve ser negativo, pois a força atua contra o movimento :
Trabalho da força de atrito:
A força de atrito também atua contra o movimento , então, seu trabalho também será negativo:
Passo 6
(e) Qual o trabalho realizado pela força peso e pela força de atrito ao longo da descida.
Essa dá pra matar rapidinho. O deslocamento na descida é o mesmo que o deslocamento na subida, certo?
Além disso, a força peso e a força de atrito vão ter o mesmo valor que antes.
Então, os trabalhos e na descida serão iguais em módulo aos trabalhos que calculamos na subida, com uma pequena diferença na análise de sinais.
Trabalho da força peso:
Agora, a forç a está atuando na mesma direção do deslocamento , então o trabalho será positivo.
Trabalho da força de atrito:
Quando o bloco começa a descer, a força de atrito vai trocar de direção, já que ela é sempre contra a tendência de deslizamento.
Então, ela continua atuando contra o movimento , logo seu trabalho será negativo:
Passo 7
(f) Qual a variação da energia cinética no trajeto total do corpo?
Lembra do teorema trabalho-energia cinética?
Ele diz que a variação da energia cinética é igual ao trabalho das forças externas sobre o corpo.
O trabalho total vai ser o trabalho da força peso mais o da força de atrito na subida e na descida.
OBS: A força Normal não faz trabalho porque é perpendicular ao movimento.
Trabalho da força peso :
Então, o trabalho total vai ser:
Trabalho da força de atrito :
Juntando tudo, temos que:
Ou seja, achamos que a variação da energia cinética é:
Faz sentido, que a variação seja negativa, já que a força de atrito vai dissipando energia ao longo do trajeto.
Resposta
(a)
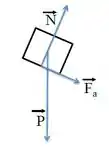
(b)
(c)
(d)
(e)
(f)