Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema Trabalho-Energia Cinética

Ver Teoria
Exercício 612345789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

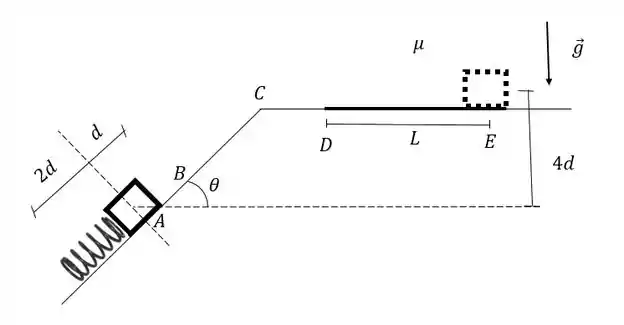
A figura mostra um sistema formado por um bloco (ou uma partícula) de massa m e uma mola de constante elástica k e comprimento de equilíbrio 3 d , ambos sob um plano inclinado que forma um ângulo θ com a horizontal. O bloco, que não está conectado à mola, está inicialmente no ponto A e comprime a mola de uma distância d . No instante inicial t = 0 , o bloco é liberado e se movimenta ao longo do plano inclinado e da base plana C D E . Há atrito apenas no trecho D E (coeficiente de atrito cinético μ k e estático μ s ), a aceleração da gravidade é g e o bloco permanece em contato com a superfície durante o movimento A C E .

a) Indique esquematicamente na figura abaixo as forças que atuam no bloco no instante inicial

b) Determine o módulo da velocidade do bloco v B no ponto B

c) Determine o módulo da velocidade do bloco v C no ponto C

d) Dado que o bloco entra em repouso no ponto E , calcule o coeficiente de atrito do trecho DE em termos de m ,   g ,   k ,   d e L .

Passo 1

a)

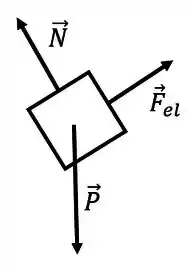
Inicialmente sobre o bloco temos as forças Normal, Peso e a força elástica da mola. O diagrama de forças fica

Passo 2

b)

No ponto B a mola estará relaxada, logo não haverá energia potencial elástica.

U e l B = 0

Já no ponto A a mola está comprimida uma distância d , logo nesse ponto a energia potencial elástica é

U e l A = 1 2 k d 2

Passo 3

Vamos definir como nível de referência a linha tracejada horizontal, logo no ponto A a energia potencial gravitacional será nula

U g A = 0

Já o ponto B está a uma certa altura h B desse nível de referência, de forma que

U g B = m g h B

A distância entre os pontos A e B é d e pra achar a altura h b podemos usar o seguinte triângulo retângulo

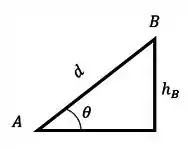
Fazendo o seno de θ

s e n θ = h B d → h B = d s e n ( θ )

Assim

U g B = m g d s e n ( θ )

Passo 4

Inicialmente o bloco está em repouso, logo a energia cinética em A é nula

K A = 0

Já no ponto B o bloco tem uma velocidade v B que queremos descobrir, então a sua energia cinética será

K B = 1 2 m v B 2

Passo 5

Pela conservação da energia mecânica

E A = E B

K A + U e l A + U g A = K B + U e l B + U g B

0 + 1 2 k d 2 + 0 = 1 2 m v B 2 + 0 + m g d s e n θ

v B 2 = k d 2 m - 2 g d s e n θ

v B = k d 2 m - 2 g d s e n θ

Passo 6

c)

No ponto C teremos energia cinética e potencial gravitacional já que a altura desse ponto em relação ao nível de referência é 4 d

E C = 1 2 m v C 2 + m g ( 4 d )

Pela conservação de energia mecânica

E A = E C

1 2 k d 2 = 1 2 m v C 2 + 4 m g d

v C 2 = k d 2 m - 8 g d

v C = k d 2 m - 8 g d

Passo 7

d)

Ao longo do trecho D E o atrito irá realizar trabalho sobre o bloco até ele parar. Como os dois pontos, D e E estão a mesma altura, só temos que nos importar a variação de energia cinética.

No ponto D a velocidade do bloco será v C que achamos no ponto anterior e no ponto E será nula.

Pelo teorema trabalho-energia cinética

W F a t = Δ K

- F a t L = K E - K D = 0 - 1 2 m v C 2

F a t L = 1 2 m v C 2

Passo 8

Já a F a t é dada por

F a t = μ s N

Como a normal se anula com o peso

F a t = μ s P = m g μ s

Assim

F a t L = 1 2 m v C 2 → m g μ s L = 1 2 m k d 2 m - 8 g d

μ s = 1 2 g L k d 2 m - 8 g d

Resposta

a)

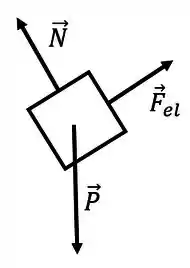
b)

v B = k d 2 m - 2 g d s e n θ

c)

v C = k d 2 m - 8 g d

d)

μ s = 1 2 g L k d 2 m - 8 g d

Exercícios de Livros Relacionados

Um caixote de 230k g está pendurado na extremidade de uma corda de comprimento L = 12,0m . Você empurra o caixote horizontalmente com uma força variável F → , deslocando-o para o lado de uma distância
Se um carro com uma massa de 1200k g viaja a 120k m / h em uma rodovia, qual é a energia cinética do carro medida por alguém que está parado no acostamento?
A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são F 1=
Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto x=+ 4,0c m , devemos aplicar uma força de 360N para mantê-lo nessa posição. Puxamos o bloco para o ponto x=11c m
No arranjo da Fig. 7-9, puxamos gradualmente o bloco de x= 0 até x=+3,0c m , onde fica em repouso. A Fig. 7-34 mostra o trabalho que nossa força realiza sobre o bloco. A escala vertical do gráfico é d