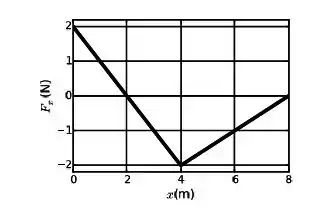
A componente de um força (em newtons) em função da posição (em metros) que atua sobre um corpo enquanto este se desloca ao longo do eixo é representada na figura abaixo. Sabe-se que em o corpo se encontra em repouso. A energia cinética em é igual a:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Sabe-se que, pela conservação da energia cinética:
E também sabemos que:
O que nesse caso se transforma em:
Passo 2
Com o corpo em repouso em , calculando as integrais como as áreas dos triângulos no gráfico, e observando a mudança de sinal, podemos dizer que:
Resposta
(e)
Exercícios de Livros Relacionados
Um caixote de 230k g está pendurado na extremidade de uma corda de comprimento L = 12,0m . Você empurra o caixote horizontalmente com uma força variável F → , deslocando-o para o lado de uma distância
Se um carro com uma massa de 1200k g viaja a 120k m / h em uma rodovia, qual é a energia cinética do carro medida por alguém que está parado no acostamento?
A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são F 1=
Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto x=+ 4,0c m , devemos aplicar uma força de 360N para mantê-lo nessa posição. Puxamos o bloco para o ponto x=11c m
No arranjo da Fig. 7-9, puxamos gradualmente o bloco de x= 0 até x=+3,0c m , onde fica em repouso. A Fig. 7-34 mostra o trabalho que nossa força realiza sobre o bloco. A escala vertical do gráfico é d