Trabalho e Energia Cinética
Dois trenós apostam uma corrida sobre um lago congelado sem atrito. Os trenós possuem massas e , respectivamente. A vela de um trenó é idêntica à do outro, de modo que o vento exerce a mesma força constante sobre cada trenó. Os dois trenós partem do repouso e a distância entre a partida e a linha de chegada é igual a . Qual a razão entre a energia cinética do trenó e a energia cinética do trenó , na reta de chegada?
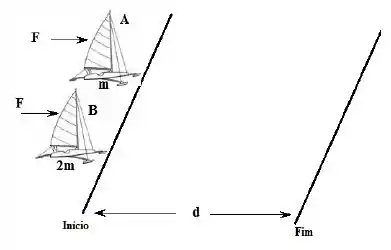
Passo 1
Para determinar a energia cinética de cada trenó na reta da chegada, devemos utilizar o teorema do Trabalho – Energia Cinética:
No caso de ambos os trenós, temos que o trabalho será:
Como ambos os trenós partem do repouso, temos que a energia cinética final de ambos será:
Portanto, temos que a razão será:
Resposta
Exercícios de Livros Relacionados
Um caixote de 230k g está pendurado na extremidade de uma corda de comprimento L = 12,0m . Você empurra o caixote horizontalmente com uma força variável F → , deslocando-o para o lado de uma distância
Se um carro com uma massa de 1200k g viaja a 120k m / h em uma rodovia, qual é a energia cinética do carro medida por alguém que está parado no acostamento?
A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são F 1=
Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto x=+ 4,0c m , devemos aplicar uma força de 360N para mantê-lo nessa posição. Puxamos o bloco para o ponto x=11c m
No arranjo da Fig. 7-9, puxamos gradualmente o bloco de x= 0 até x=+3,0c m , onde fica em repouso. A Fig. 7-34 mostra o trabalho que nossa força realiza sobre o bloco. A escala vertical do gráfico é d