Um bloco de é mantido contra uma mola de massa desprezível cuja constante elástica é e que sofre uma compressão de . O bloco é liberado do repouso no ponto A e a mola projeta o bloco por um plano inclinado ascendente cujo ângulo com a horizontal é . O bloco atinge o repouso momentâneo no ponto B. Desprezam-se as forças de atrito. Admita que o bloco perca contato com a mola quando esta está relaxada.
- Faça um diagrama das forças atuando no bloco em algum momento antes de se desprender da mola.
- Utilizando o teorema do trabalho-energia, qual a distância, ao longo do plano inclinado, entre o ponto A e o ponto B?
- Quando o bloco desliza de volta para baixo, qual é a sua velocidade no ponto médio do caminho entre A e B? (Dado: utilize se necessário)
Passo 1
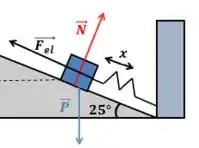
Bom galera, antes de começarmos, vamos fazer um desenho geral do problema:
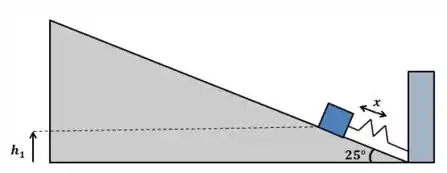
Passo 2
a):
As forças que agem no bloco são:
- Força elástica:
- Peso:
- Normal:
A força peso sempre aponta pra baixo, a força elástica tem a direção do plano e a força normal é perpendicular à superfície, então:
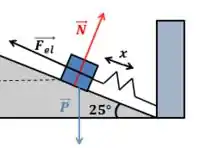
Passo 3
b):
Bom, o enunciado nos diz pra gente usar o teorema trabalho-energia nesse caso. Vamos usar a versão desse teorema que temos na nossa teoria:
Ou seja, a variação da energia mecânica é igual ao trabalho das forças não-conservativas.
No entanto, a única força não conservativa ali é a normal. E a normal não realiza trabalho, já que é perpendicular à trajetória. Então:
Ou seja, como a variação da energia mecânica é zero, ela se conserva.
Então, daqui em diante vamos usar a conservação da energia mecânica pra achar a distância que o enunciado pede.
Passo 4
Bom, conforme a figura:
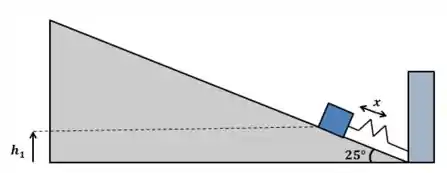
No instante inicial, a caixa estava em uma altura e a mola estava contraída em metros.
Então, a energia mecânica inicial é:
Beleza?
Bom, após a caixa se desprender da mola, ela vai se deslocar um pouco, até parar. Quando ela parar, ela terá atingido uma altura , e sua energia mecânica será toda potencial gravitacional:
Como a energia mecânica final é igual à inicial:
Vamos chamar essa diferença de altura ai de
Mas essa medida é tomada na vertical, já que é uma diferença entre alturas. Nós queremos saber a distância percorrida ao longo do plano inclinado.
Bom, ai é só a gente lembrar que a relação entre essa distância e a distância percorrida no plano é a mesma relação entre cateto e hipotenusa:
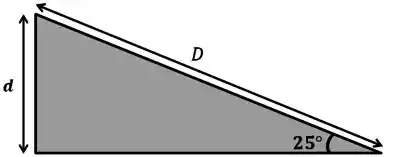
Queremos achar . Só que:
Então:
Substituindo os valores dados no enunciado:
Passo 5
c):
Bom, essa aqui é bem tranquila, basta a gente usar a conservação da energia entre a altura e
Resposta
a):
b):
c):