Um corpo de massa move-se apenas sobre o eixo . Na origem, sua velocidade vale , e o gráfico a seguir mostra a variação da força resultante que atua sobre o corpo.
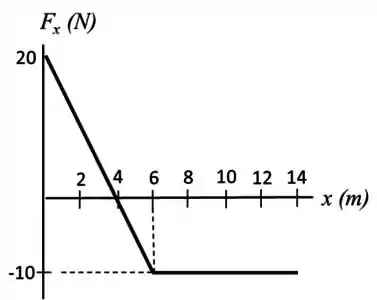
Qual a energia cinética do corpo, e qual a sua velocidade em ?
Responda, justificando, para que valor de a energia cinética do corpo é máxima? Quanto vale sua velocidade aí?
Para qual (ou quais) valor(es) de a velocidade instantânea do corpo vale ?
Passo 1
Quando temos um gráfico de força por deslocamento, devemos sempre lembrar que a área abaixo da curva é igual ao trabalho!
Para calcular a energia cinética em , precisamos utilizar o teorema do trabalho e energia cinética, ele nos diz:
Passo 2
Para calcular o trabalho, precisamos calcular a área abaixo da curva entre e :
Teremos o triângulo, entre e :
E o trapézio entre e :
O trabalho será então:
Lembrando que curvas abaixo do eixo, como , contribuem negativamente!
Passo 3
Voltando à equação da variação de energia, temos:
Onde é a energia cinética do corpo em . Substituindo os valores conhecidos, temos:
Agora que temos a energia cinética, determinar a velocidade é fácil, se liga!
Substituindo os valores, temos:
Passo 4
Pelo teorema do trabalho e energia cinética, podemos ver que a variação da energia cinética será positiva, ou seja ela irá aumentar até quando o trabalho for positivo. Desse modo, podemos ver pelo gráfico que isso ocorrerá até , que é onde o trabalho passa de positivo para negativo.
Já calculamos, no item , o trabalho realizado de 4, ele vale . Pelo teorema, temos:
Substituindo os valores, temos:
Passo 5
Para determinar os valores de em que a velocidade instantânea é vamos utilizar o mesmo teorema, só que agora faremos um caminho um pouco diferente. Temos a velocidade, ou seja, podemos calcular a variação da energia cinética. E com isso encontraremos para que valor de trabalho temos essa variação. Se liga!
Substituindo os valores conhecidos, temos:
Ou seja, os pontos em que a velocidade instantânea é , são aqueles em que o trabalho é .
Passo 6
Sabemos que existe um ponto desses entre e , pois em , o trabalho vale Utilizaremos novamente a área, sabendo que seu valor deve ser .
Para qualquer valor antes de , a área abaixo da curva será a de um trapézio. Para achar o valor de , precisamos determinar e quação da curva, pois somente dessa maneira teremos a base menor do trapézio, se liga!
Para determinar a equação da curva, é só substituir dois ponto, desse modo, acharemos:
A área do trapézio será dada por:
Igualando a , temos:
Acharemos como solução dessa equação, os valores:
Desses valores, somente é válido, pois depois de , o comportamento da curva muda.
Passo 7
Vamos agora analisar a existência de um ponto onde o trabalho seja depois de . Sabemos que a partir de , o comportamento da curva muda, em , temos que o trabalho é:
Depois de , a área será dada por um retângulo, precisamos então, achar para que valor de , a área desse retângulo será igual a , pois !
Igualando a , temos:
Pronto, temos que a velocidade instantânea do corpo será igual a para os eguintes valores de :
Resposta
;
;