Um bloco de massa repousa sobre uma mesa de altura , e comprime uma mola de constante contra a parede. No instante inicial o bloco está em repouso a uma distância da extremidade da mesa, e a compressão da mola é igual a (em relação à sua posição de equilíbrio). O bloco é então liberado, desliza até a extremidade da mesa e cai no chão (vide figura). O coeficiente de atrito cinético entre o bloco e a mesa é .
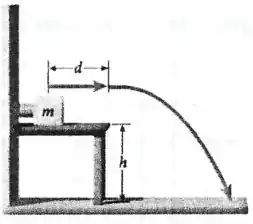
a) Faça o diagrama das forças para o bloco quando o mesmo desliza sobre a mesa, antes de perder o contato com a mola; e durante a queda.
b) Qual é o trabalho realizado pela força de atrito?
c) Qual é o módulo da velocidade com que o bloco chega ao chão?
d) Qual seria o módulo da velocidade com que o bloco chegaria ao chão se não houvesse atrito entre o bloco e a mesa?
Passo 1
a)
Basta ficar atenção ao sentido da força de atrito e da força elástica, a figura vai ficar assim:
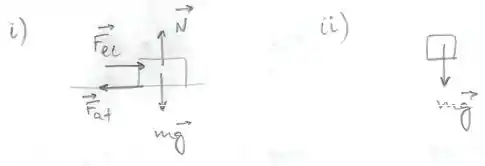
Passo 2
b)
Utilizando a fórmula do trabalho e da força de atrito:
Passo 3
c)
Utilizando o teorema Trabalho – Energia, sabemos que a variação da energia cinética é igual ao somatório de todos os trabalhos realizados.
Passo 4
d)
Podemos utilizar o valor que achamos no item anterior e dizer que , que é o mesmo que dizer que não tem atrito. Vamos ter então:
Resposta
a)
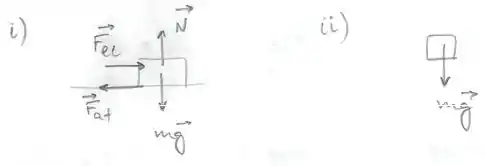
b)
c)
d)