Um bloco está em repouso sobre um plano inclinado muito longo. A inclinação do plano é de com a horizontal. Repentinamente uma força impulsiva atua sobre o bloco em direção à base do plano, produzindo uma velocidade inicial de . O bloco para após percorrer . Qual é o valor do coeficiente de atrito cinético entre o bloco e o plano?

Passo 1
Vamos fazer um diagrama do bloco no momento inicial pra visualizar melhor a questão, ok? Podemos definir o eixo no sentido do plano inclinado, dessa forma o eixo fica na direção da força normal:
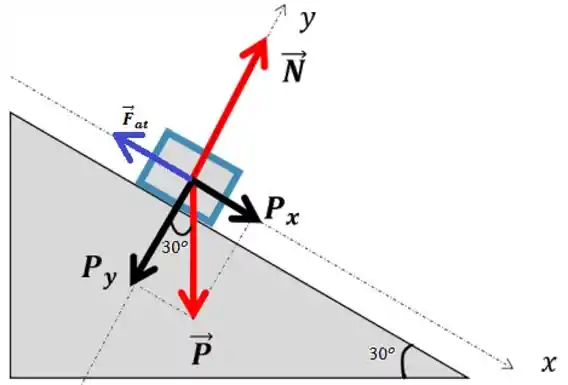
então com um uma trigonometria básica obtemos
Como não há deslocamento no eixo , e se equivalem:
Passo 2
Uma boa pedida é aplicar o teorema trabalho-energia cinética:
Primeiro vamos tentar calcular , o trabalho total aplicado sobre o bloco, beleza?
Mas primeiro precisamos saber o quanto o bloco desceu!
Sabemos que ele andou em um plano inclinado de em relação à horizontal, então ele desceu :
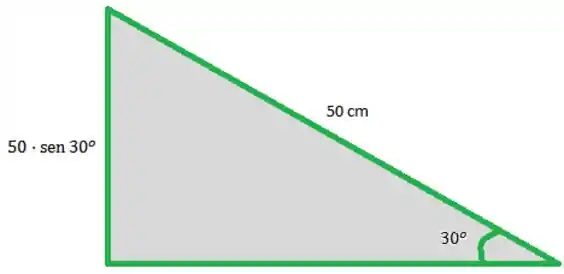
Passo 3
Show, vamos calcular o trabalho!
Há 3 forças atuando no bloco: o peso, a normal e a força de atrito.
A normal nós sabemos que não realiza trabalho por ser ortogonal ao sentido de deslocamento do bloco.
O trabalho da força peso é
sendo a altura que ele desceu, que é
Ou seja:
Passo 4
A força de atrito é
sendo o coeficiente de atrito cinético e a força normal.
A força de atrito é contrária ao deslocamento, então o trabalho é negativo:
Vimos lá atrás que , logo:
Portanto,
Passo 5
Agora vamos calcular a diferença de energia cinética!
A velocidade inicial do bloco é então sua energia cinética inicial é:
E o bloco termina o movimento no repouso, portanto sua energia cinética final é nula.
Então
Passo 6
Ótimo! Finalmente podemos aplicar o teorema trabalho-energia cinética:
Substituindo o que achamos antes:
Passo 7
Temos
Obs: se você quiser, pode substituir pelos valores que e o enunciado dá, tipo mas eu acho que nem ajuda muito.
Além disso, podemos também substituir , o que dá: