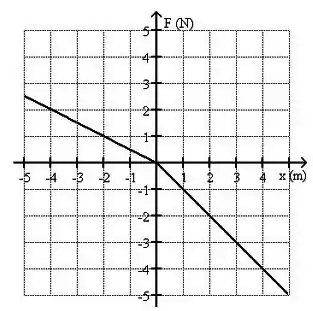
Uma partícula de massa move-se ao longo do eixo sujeita a uma força que varia com a posição conforme o gráfico ao lado. Se a velocidade da partícula é quando ela passa por , qual é a sua velocidade quando ela passa por ?
(a)
(b)
(c)
(d)
(e)
Passo 1
Podemos relacionar a variação de energia cinética com o trabalho realizado por esta força no percuso
Pelo gráfico temos dois trechos. O primeiro é de até
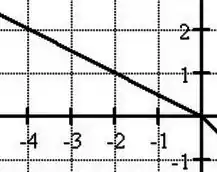
Nesse trecho o trabalho é dado pela área abaixo da curva. Essa área é a área de um triângulo
O segundo trecho é de até
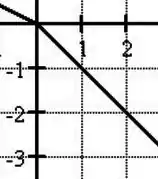
Nesse trecho o trabalho vai ser dado por MENOS a área do triângulo correspondente porque a força é negativa
Assim o trabalho total é
Passo 2
Agora podemos relacionar a variação de energia cinética com o trabalho feito por
Como a energia cinética é
Substituindo os valores que temos
Resposta
(C)