Um objeto de massa possui, em um certo instante escolhido como , uma energia cinética de e se move em uma dimensão, escolhida como o eixo OX. O gráfico abaixo representa a força resultante a que está submetido o objeto.
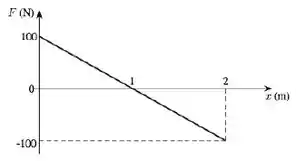
Sobre a energia cinética do objeto quando chega à posição é correto afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Passo 1
Cálculo de :
De acordo com o Teorema Trabalho Energia Cinética, temos:
Ao calcularmos a área do gráfico, encontraremos o trabalho realizado pela força.
Calculando
Logo,
Resposta
Exercícios de Livros Relacionados
Um caixote de 230k g está pendurado na extremidade de uma corda de comprimento L = 12,0m . Você empurra o caixote horizontalmente com uma força variável F → , deslocando-o para o lado de uma distância
Se um carro com uma massa de 1200k g viaja a 120k m / h em uma rodovia, qual é a energia cinética do carro medida por alguém que está parado no acostamento?
A Fig. 7-26 mostra uma vista superior de três forças horizontais atuando sobre uma caixa que estava inicialmente em repouso e passou a se mover sobre um piso sem atrito. Os módulos das forças são F 1=
Uma mola e um bloco são montados como na Fig. 7-9. Quando o bloco é puxado para o ponto x=+ 4,0c m , devemos aplicar uma força de 360N para mantê-lo nessa posição. Puxamos o bloco para o ponto x=11c m
No arranjo da Fig. 7-9, puxamos gradualmente o bloco de x= 0 até x=+3,0c m , onde fica em repouso. A Fig. 7-34 mostra o trabalho que nossa força realiza sobre o bloco. A escala vertical do gráfico é d