Um pêndulo simples é formado por uma massa , presa a um fio ideal de comprimento , que tem uma de suas extremidades presa a um suporte no teto. O pêndulo é abandonado, em repouso, na posição horizontal. As forças que atuam no pêndulo são o peso, a tração e a resistência do ar. O pêndulo realiza seu movimento conforme a trajetória pontilhada até inverter o seu movimento, quando faz um ângulo com a vertical, conforme a figura.
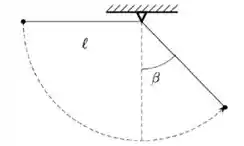
Qual o trabalho realizado pela força de resistência do ar no deslocamento entre os instantes em que o pêndulo é abandonad e aquele no qual ele faz o ângulo com a vertical, indicado na figura?
a)
b)
c)
d)
e)
f)
g)
Passo 1
Pra gente começar a gente já pode ficar ligado que como se trata de uma força de resistência, o trabalho é negativo. É como se fosse uma força de atrito, sabe? Só ai já da pra eliminar umas opções.
Nós temos três forças atuando no sistema:
Tração: não realiza trabalho, porque sua força é sempre perpendicular à trajetória
Peso: força conservativa
Força de resistência: o que a gente está querendo descobrir.
Então se nós descobrirmos a diferença de energia entre os dois pontos que ele pede vamos saber que a diferença é o trabalho da força de resistência
Passo 2
Como nos dois pontos ele está parado, não vamos ter energia cinética.
Diminuindo os dois pontos ficamos com o trabalho da resistência do ar: