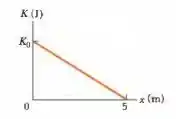
(Capítulo 7.5 – Exercício 12) Um objeto de está se movendo no sentido positivo de um eixo . Quando passa pelo ponto , uma força constante dirigida ao longo do eixo passa a atuar sobre ele. A Fig. 7-28 mostra a energia cinética em função da posição quando o objeto se desloca de a ; . A força continua a agir. Qual é a velocidade do objeto no instante em que passa pelo ponto ?
Passo 1
Shoow galerinhaaa, vamos lá resolver esse exercício
Bom, se a velocidade está mudando, isso significa que existe uma aceleração que está sendo aplicada ao corpo! Então nós precisamos achá-la certo? Para aí depois encontrarmos a velocidade antes da força ser aplicada
A única coisa que temos é a variação da energia cinética. Podemos aplicar a fórmula dela com as informações que temos no gráfico
De onde podemos encontrar , onde é a velocidade final e é a velocidade inicial
E aí, pra encontrar a aceleração sem termos o tempo podemos usar Torricelli:
Podemos usar essa mesma fórmula para encontrar a velocidade inicial , que é a velocidade em , que é quando a força começa a ser aplicada, e teremos nosso resultado final
Então vamos lá!
Passo 2
Vamos começar encontrando usando essa fórmula:
Se:
Substituindo:
Mas isso não resolve em nada nossa vida, porque queremos a aceleração
Mas podemos usar a equação de Torricelli, bora!
Passo 3
Temos
Isolando a aceleração:
Do item anterior, sabemos que
Se o objeto se desloca no gráfico, temos que :
Show, a aceleração já temos! Agora vamos usar o Torricelli de novo pra encontrar a velocidade inicial , sabendo que a velocidade final é
Passo 4
Para achar a velocidade após um certo deslocamento nós podemos usar a mesma fórmula do passo anterior:
A velocidade final nós já sabemos que é zero, porque ele não tem energia cinética:
Com isso nós podemos achar qual é a velocidade inicial do objeto:
Logo ,
Para saber a velocidade no ponto quando ,basta nós substituirmos na formula que acamos de ver, só que aqui o
Tranquilo galera??? Bora resolver mais questões então